 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Лабораторная работа №3. Численное дифференцирование сложных функций
|
|
Проведем вычисление производной сложной функции.
 (26)
(26)
Согласно правилу дифференцирования сложной функции: ее производная должна ровняться произведению производных составляющих ее функций. Разобьем функцию на составляющие, продифференцируем каждую посоответствующей переменной и перемножим. Результат сравним с приближенными разностными производными, вычисленными по формулам (4)-(6). Близость полученных значений проиллюстрирует теорему о производной сложной функции.
Представим функцию (26) следующим образом:
 (27)
(27)
 (28)
(28)
 (29)
(29)
По теореме о производной сложной функции
 (30)
(30)
где
 (31)
(31)
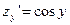 (32)
(32)
 (33)
(33)
Для выполнения задания:
§ осуществите запуск программы Excel;
§ откройте файл, в котором выполнялась первая и вторая лабораторные работы;
§ выполните следующее.
Создание таблицы.
1. Сделайте еще одну копию Листа2 - Лист2(4) - так, как описано в лабораторной работе 6.
2. На новом листе перед столбцом D вставьте новые шесть столбцов. Для этого выделите столбец D и выполните шесть раз команду меню ВСТАВКА ‑ СТОЛБЦЫ.
3. Смените заголовок таблицы так, чтобы он имел вид как на рисунке 54. Для верхних и нижних индексов воспользуйтесь указаниями лабораторной работы 5 для заголовка на рисунке 33.

Рис. 54
4. Сдвиньте в таблице границы отрезка [а, b] на 0,05 вправо, т.е. в ячейки А2, A3 запишите значения 0,05 и 1,1 соответственно.
5. Чтобы записать в ячейку С2 сложную функцию (26) вызовите команду ВСТАВКА ФУНКЦИИ и на первом шаге выберите функцию КОРЕНЬ. На втором шаге, на котором надо выбирать аргумент, откройте список функций в строке формул и выберите SIN (см. рис. 55), в качестве аргумента SIN запишите B2^2.
|


Рис. 55
6. В ячейки D2:I2 новых столбцов впишите функции Excel, соответствующие функциям 29, 28, 27, 31, 32, 33, т.е.
D2: = B2^2 G2: =2*В2
Е2: = SIN(D2) H2: =COS(D2)
F2: = КОРЕНЬ(Е2) I2: =0.5/КОРЕНЬ(Е2).
7. Согласно теореме о производной сложной функции (30) в ячейку J2 запишите формулу =G2*H2*I2.
8. Выделите ячейки C2:J2 и с помощью маркера заполнения заполните формулами строчки вниз вплоть до 23 строки.
В результате выполненных действий изменится вся таблица и графики диаграммы. Сравнение значений производных, а, в особенности, графики хорошо иллюстрируют теорему о производной сложной функции. Часть полученной таблицы и диаграмма выглядят так:


Рис. 56
В качестве самостоятельной работы рассчитайте производную функции
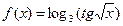 (34)
(34)
разбив ее как функцию (26) на три, вложенные друг в друга функции. Построение выполните на листе, полученном как копия листа Лист2(4). Функция (34) в ячейке С2 будет иметь вид: 
Часть итоговой таблицы и диаграмма представлены на рисунке 57.


Рис. 57
В заключение предлагается построить график производной сложной функции, которая выражена через исходный аргумент Х. Для этого используйте копию листа Лист2(1), который применялся в лабораторной работе № 6. Рассмотрите функцию
 . (35)
. (35)
Так как функция определена при х> 1, в столбец А занесите границы отрезка [1,05; 2,1]. Функция (35) в ячейке С2 будет иметь вид
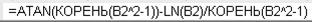
Рассчитайте производную и запишите полученную формулу в столбец D. Таблица и график функции (35) показаны на рисунке 58.

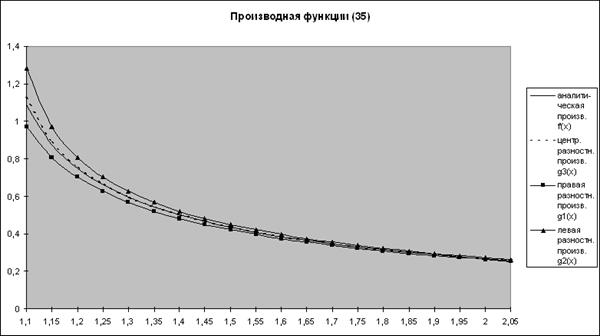
Рис. 58
Сохраните все внесенные в файл изменения, выполнив команду меню ФАЙЛ - СОХРАНИТЬ или воспользовавшись кнопкой панели инструментов  . Закончите работу в Excel.
. Закончите работу в Excel.
Дата публикования: 2014-11-18; Прочитано: 1136 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
