Примеры решения задач. Задача12.3.1. Груз 3 массы т3 поднимается лебедкой, приводя­щейся в движение электромотором А (рис

Задача12.3.1. Груз 3 массы т ₃ поднимается лебедкой, приводя­щейся в движение электромотором А (рис. 12.1). Передача движения от вала I на вал II осуществляется с помощью пары зубчатых колес 1 и 2. Трос, к концу которого прикреплен груз, наматывается на бара­бан В радиуса r. Определить закон изменения угловой скорости вала I, если со стороны электромотора на вал действует вращающий момент , где М ₀ и а - положи­тельные постоянные, характеризующие мо­тор; - угловая ско­рость вала I (электромо­тора). Числа зубьев ко­лес z ₁ и z ₂, моменты инерции валов лебедки I ₁ и I ₂. Сопротивлением движению и массой троса пренебречь.

Рис. 12.1

Решение. Рассмотрим систему, состоящую из ротора электро­мотора D, лебедки и поднимаемого груза (рис. 12.2). Система имеет одну степень свободы, если тела, входящие в эту систему, абсолют­но твердые, трос нерастяжимый, а раскачивание груза при подъеме отсутствует. Система является неизменяемой, если дополнительно положить, что трос является абсолютно гибким.

Составим дифференциальное уравнение движения системы, приняв за координату, определяющую ее положение, угол поворота электромотора .

Воспользуемся теоремой об изменении кинетической энергии в дифференциальной форме

. (12.5)

Рис. 12.2

Дальнейшая последовательность действий определяется струк­турой этой формулы.

Вычислим кинетическую энергию системы как сумму кинетиче­ских энергий тел, входящих в ее состав,

. (12.6)

Кинетическая энергия вала I (имеется в виду совокупность тел: вал лебедки с колесом 1, муфта, связывающая валы электромотора и лебедки (на рисунке не показана) и ротор электромотора), вращаю­щегося с угловой скоростью :

. (12.7)

Кинетическая энергия вала II (имеется в виду совокупность тел: вал, барабан и колесо 2), вращающегося с угловой скоростью :

. (12.8)

Кинетическая энергия груза, движущегося поступательно со скоростью v _з:

. (12.9)

Подставляя (12.7)-(12.9) в формулу (12.6), получаем

. (12.10)

Воспользуемся соотношением , выражающим равен­ство скоростей точек на ободах зубчатых колес; из него находим

. (12.11)

Кроме того, , или, с учетом формулы (12.11),

. (12.12)

Подставим (12.11) и (12.12) в формулу (12.10). Поскольку отноше­ние радиусов колес r ₁ и r ₂ можно заменить отношением чисел зубьев z ₁ и z ₂, то

. (12.13)

Введем обозначение

.

и, учитывая, что , получаем

,

откуда

. (12.14)

Вычислим теперь сумму мощностей внешних сил. Из внешних сил, действующих на рассматриваемую систему, на расчетной схеме показаны только силы, мощность которых не равна нулю, - это вра­щающий момент и сила тяжести груза. Точки приложения других внешних сил (силы тяжести валов I и II со всеми деталями, силы тяжести муфты, ротора электромотора, реакций подшипников) неподвижны, поэтому мощность этих сил равна нулю. Мощность мо­мента равна , мощность силы тяжести груза

Таким образом,

,

или, учитывая (12.12), а также, что получаем

. (12.15)

Введем обозначение , тогда

. (12.16)

Приравнивая, согласно (12.5), правые части соотношений (12.14) и (12.16), получаем после сокращения на , дифференциальное урав­нение движения системы:

. (12.17)

Поскольку приведенный момент инерции является постоян­ным, а силовой момент - функция угловой скорости , то уравнение (12.17) можно записать в виде

. (12.18)

Для определения закона изменения угловой скорости перепи­шем последнее уравнение в виде

. (12.19)

Построим общее решение уравнения (12.19). Поскольку оно яв­ляется неоднородным линейным дифференциальным уравнением первого порядка, то

. (12.20)

где - общее решение однородного уравнения ; - частное решение неоднородного уравнения (12.19).

Для определения функции запишем характеристическое уравнение и найдем его корень . Следовательно,

. (12.21)

Частное решение уравнения (12.19) разыскиваем в виде

. (12.22)

Для определения постоянной А следует подставить (12.22) в уравнение (12.19):

.

Таким образом, общее решение уравнения (12.19) имеет вид

. (12.23)

Постоянную интегрирования С определим из начального усло­вия :

.

Подставляя найденное значение постоянной С в (12.23), получаем закон изменения угловой скорости первого вала

. (12.24)

Из найденного решения следует, что по истечении некоторого промежутка времени первый вал будет вращаться с постоянной угловой скоростью

.

Задача 12.3.2. Груз 3 массы т ₃ перемещается по наклонной плоско­сти, образующей угол 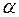с горизонтом, электрической лебедкой, со­стоящей из зубчатого колеса 1 радиуса R ₁ и находящегося с ним в зацеплении колеса 2 радиуса R ₂, на одном валу с которым находится барабан радиуса r ₂, на который навивается трос, прикрепленный к грузу (рис. 12.3).

К колесу 1 приложен со стороны мотора постоянный вращающий момент М ₁ на валу колеса 2 действует постоянный момент сопротив­ления М ₂. Определить угловую скорость колеса 1 как функцию его угла поворота, если I ₁ - момент инерции ведущего вала (вал и колесо l); I ₂- момент инерции ведомого вала (вал, ко­лесо 2 и барабан); f -коэффициент трения скольжения груза о наклонную плоскость. Трос считать нерастя­жимым, невесомым и не сопротивляющим­ся изменению формы. Движение начинается из состояния покоя. Центры масс вращаю­щихся тел находятся на осях вращения.

Рис. 12.3

Решение. Рассмотрим систему, состоящую из тел 1-3 и троса. Поскольку тела абсолютно твердые, а трос нерастяжимый, то систе­ма имеет одну степень свободы. Будем определять положение сис­темы с помощью угла поворота ведущего вала. Заметим также, что система является неизменяемой. Поскольку движение системы происходит под действием постоянных сил, работу которых можно вычислить, не зная закона движения системы, то для решения задачи удобно использовать теорему об изменении кинетической энер­гии в конечной форме для неизменяемых систем

. (12.25)

Определим приращение кинетической энергии системы на пе­ремещении из начального положения в некоторое конечное, зада­ваемое углом . Кинетическая энергия системы в начальном поло­жении Т ₀= 0 (по условию). Кинетическая энергия системы в конеч­ном положении равна сумме кинетических энергий ведущего и ве­домого валов и груза:

,

где - угловая скорость ведущего и ведомого валов соответст­венно; v ₃ - скорость груза (рис. 12.4).

Рис. 12.4

Поскольку

,

то

,

или

,

где

.

Таким образом, приращение кинетической энергии системы на рассматриваемом перемещении найдено как функция угловой ско­рости ведущего вала в конечном положении:

. (12.26)

Внешними силами, действующими на систему, являются вра­щающий момент М ₁ момент сопротивления М ₂, силы тяжести тел , реакции подшипников ведущего вала , реакции под­шипников ведомого вала и реакции плоскости: сила трения 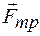и нормальная реакция . Вычислим теперь работу внешних сил на перемещении системы из начального положения в конечное:

1) работа вращающего момента равна ;

2) работа момента сопротивления равна , где -угол поворота ведомого вала;

3) работы сил , а также , равны нулю, так как эти силы приложены в неподвижных точках;

4) работа силы равна нулю, так как эта сила перпендику­лярна перемещению точки ее приложения;

5) работа силы равна , где s ₃ - перемещение груза;

6) работа силы трения равна (), где .

Таким образом,

.

Но

,

поэтому

.

или

, (12.27)

где

.

Приравнивая, согласно (12.25), правые части формул (12.26) и (12.27), получаем

,

откуда

. (12.28)

Таким образом, искомая зависимость имеет вид:

.

Вопросы для самоконтроля

(защиты контрольной работы)

1. Что называется кинетической энергией материальной точки?

2. Что называется кинетической энергией механической системы?

3. Сформулируйте теорему Кенига.

4. Получите формулы для вычисления кинетической энергии твердого тела при поступательном, вращательном и плоско­параллельном его движениях.

5. Как вычисляется работа силы упругости и силы тяжести?

6. На каких перемещениях работа силы тяжести а) положительна, б) отрицательна, в) равна нулю?

7. При каких условиях работа силы упругости положительна; отрицательна?

8. Как определяется работа постоянной по модулю и направле­нию силы на прямолинейном перемещении?

9. Чему равна работа постоянной по модулю и направлению силы трения скольжения?

10. Что называется мощностью силы?

11. Как определяется работа и мощность силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси?

12. Сформулируйте теорему об изменении кинетической энергии механической системы в дифференциальной форме (в форме мощностей).

13. Сформулируйте теорему об изменении кинетической энергии механической системы в конечной (интегральной) форме.