Примеры решения задач. Задача 8.2.1. Составить дифференциальное уравнение движения механической системы, состоящей из груза 1

Задача 8.2.1. Составить дифференциальное уравнение движения механической системы, состоящей из груза 1, блока 2 и катка 3, имеющих соответственно массы т ₁, т ₂, т ₃, и пружины с коэффици­ентом жесткости с (рис. 13.1). Груз и каток, расположенные на наклонных плоскостях, составляющих с горизонтом углы 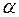и , связаны невесомой и нерастяжимой нитью, перекинутой через блок. Тре­нием груза о плоскость, массой пружины и сопротивлением каче­нию пренебречь. Проскальзывание нити на блоке отсутствует. Каток катится без скольжения. Блок считать однородным цилиндром, мо­мент инерции катка относительно центральной оси равен , радиусы ступеней катка R и r.

Решение. Рассматриваемая система имеет одну степень свобо­ды при выполнении следующих условий:

1. Тела, входящие в систему, абсолютно твердые.

2. Нить нерастяжимая и при движении системы всегда натянута.

3. Проскальзывание нити на блоке отсутствует.

4. Каток катится без скольжения.

Рис. 13.1

Будем определять положение системы с помощью координаты х, направив соответствующую ось Ох параллельно наклонной плос­кости, на которой расположен груз. Начало оси совместим с поло­жением центра масс груза при равновесии системы (рис. 13.2). Пусть , и - соответствующие координате х углы поворота блока и катка и смещение центра масс катка от положения его равновесия.

(13.3)

где - радиус блока.

Для составления дифференциального уравнения движения вос­пользуемся общим уравнением динамики. Построим расчетную схему задачи. Изобразим на рисунке активные силы , , , реакцию неидеальной связи (пружины) ; приложим к телам сис­темы силы инерции.

Рис. 13.2

Груз движется поступательно. Силы инерции его частиц эквива­лентны равнодействующей

, (13.4)

приложенной в центре масс ( - ускорение груза).

Блок вращается вокруг главной центральной оси инерции. Силы инерции его частиц эквивалентны паре сил с моментом

, (13.5)

где - момент инерции блока относительно оси вращения.

Вектор направлен по оси вращения блока противоположно вектору углового ускорения . На расчетной схеме это отражено дуговыми стрелками противоположного направления.

Каток совершает плоское движение. Силы инерции его частиц эквивалентны системе, состоящей из одной силы

, (13.6)

приложенной в центре масс катка ( - ускорение центра масс), и пары сил с моментом

, (13.7)

где - угловое ускорение катка.

Сообщим грузу возможное перемещение . Возможным пере­мещением блока является поворот на угол вокруг собственной оси. Возможным перемещением катка является поворот на угол вокруг оси, проходящей через мгновенный центр скоростей Р ₃ пер­пендикулярно плоскости рисунка. Векторы и направлены по соответствующим осям, на расчетной схеме направления воз­можных поворотов блока и катка показаны дуговыми стрелками.

Запишем общее уравнение динамики

. (13.8)

Заметим, что элементарная работа силы равна нулю, так как равно нулю возможное перемещение точки ее приложения.

Подставив в уравнение (13.8) формулы (13.4)-(13.7) и раскрыв ска­лярные произведения, получим

. (13.9)

Используя формулы (13.3), находим

(13.10)

(13.11)

Подставляя формулы (13.10) и (13.11) в уравнение (13.9), находим после сокращения на и простых преобразований:

(13.12)

Из уравнения (13.12) легко получить условие равновесия систе­мы. Действительно, поскольку

, (13.13)

где - статическая деформация пружины, то, подставляя (13.13) в уравнение (13.12) и имея в виду, что при равновесии x = 0, = 0, на­ходим

. (13.14)

С учетом условия (13.14) уравнение (13.12) принимает вид

(13.15)

Назовем приведенной массой и приведенной жесткостью величины

.

Тогда дифференциальное уравнение (13.15) можно записать в виде

, (13.16)

где

.

Задача 8.2.2. Груз 3 массы т ₃ поднимается с помощью устройства, состоящего из шкивов 1 и 2, связанных невесомым ремнем (рис. 13.3). К ведущему шкиву 1 радиуса R ₁ при­ложена пара сил с посто­янным моментом М. Оп­ределить угловое уско­рение ведущего шкива, если R ₂, r ₂ - радиусы ступеней ведомого шки­ва; I ₁ и I ₂ - моменты инерции шкивов относи­тельно осей их вращения. Сопротивлением и мас­сой троса пренебречь.

Рис. 13.3

Решение. Рассмат­риваемая механическая система имеет одну степень свободы, если выполняются следующие условия:

1. Тела 1, 2, 3 - абсолютно твердые.

2. Ремень и трос нерастяжимые.

3. Проскальзывание ремня на шкивах отсутствует.

4. Груз поднимается, не раскачиваясь (по направляющим).

Построим расчетную схему задачи. Связи, наложенные на сис­тему, являются идеальными. Поэтому на расчетной схеме (рис. 13.4) показаны только активные силы (вращающий момент и силы тяже­сти тел) и силы инерции.

Рис. 13.4

Шкив 1 вращается вокруг своей главной центральной оси инер­ции. Поэтому система сил инерции его частиц эквивалентна паре сил, момент которой направлен противоположно угловому ускоре­нию шкива 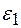и имеет величину

. (13.17)

Шкив 2 также вращается вокруг своей главной центральной оси инерции. Поэтому система сил инерции его частиц эквивалентна паре сил, момент которой направлен противоположно угловому ускорению шкива 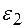и имеет величину

. (13.18)

Груз движется поступательно. Система сил инерции частиц гру­за эквивалентна равнодействующей силе, которая приложена в цен­тре масс, направлена противоположно его ускорению и имеет вели­чину

. (13.19)

Сообщим шкиву 1 возможное перемещение . Шкив 2 и груз 3 получат при этом возможные перемещения и соответствен­но. Запишем общее уравнение динамики

. (13.20)

Нетрудно установить, что

, (13.21)

. (13.22)

Подставив формулы (13.17)-(13.19), (13.22) в уравнение (13.20), по­лучим, с учетом (13.21), уравнение

.

из которого, после сокращения на находим

.