Критерий однородности Лемана-Розенблатта

Критерий однород­но­сти Лемана-Розенблатта представляет собой критерий типа . Критерий был предложен в работе [10] и исследован в [11]. Статистика критерия имеет вид [3]

,

где 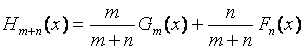– эмпирическая функция распре­де­ления, построенная по вариационному ряду объединения двух выборок. Статистика T используется в форме [3]

, (3)

где r_i – порядковый номер (ранг) y_i, s_j – порядковый номер (ранг) x_j в объе­диненном вариационном ряде.

В [11] было показано, что статистика (3) в пределе распределена как :

.

В отличие от статистики критерия Смирнова распределение статистики T быстро сходится к предельному [3]. Наши результаты моделирования условных распределений ста­ти­стики (3) при различных объемах выборок показали, что уже при распределение статистики очень близко к , а при и практически совпадает с ним.

Рис. 5 иллюстрирует полученные в результате моделирования ус­ловные распределения статистики при справедливости H1. На основа­нии этих распределений можно оценить значения мощности критерия Лемана-Ро­зенблатта при различных значениях объемов выборок m,n.

Рис. 5. Распределения статистики (3) при справедливости H1.

Аналогичным образом были построены распределения статистики , , , при справедливости соответ­ству­ю­щих конкурирующих гипотез. Вычисленные значения мощности крите­рия Лемана-Розенблатта представлены в таблице 3.

Вывод

Сравнивая мощность критериев относительно рассмот­ренных альтернатив с учетом действительных уровней значимости критерия Смирнова (табл. 2), можно заметить, что, как правило, мощность критерия Лемана-Розенблатта заметно выше мощности критерия Смирнова. Однако относительно очень близких альтернатив несколько выше оказы­вается мощ­ность критерия Смирнова (см. мощность относительно альтернативы H5). По­следнее становится интуитивно понятным, если вспомнить, что в крите­рии Смирнова мера отклонения линейная, а в критерии Лемана-Розенблатта – квадратичная.

Таблица 3. Мощность критерия однородности Лемана–Розенблатта относи­тель­но альтернатив H1÷H5 в зависимости от объемов выборок (m=n)

Уровень значимости	Значения мощности относительно альтернативы
n=20	n=50	n=100	n=300	n=500	n=1000	n=2000
0,1	0,1241	0,1382	0,1727	0,3125	0,4369	0,6874	0,9114
0,05	0,0615	0,0770	0,0999	0,2078	0,3211	0,5703	0,8469
0,025	0,0324	0,0410	0,0590	0,1333	0,2288	0,4589	0,7681
	Значения мощности относительно альтернативы
0,1	0,4321	0,7628	0,9549
0,05	0,3121	0,6473	0,9154
0,025	0,2120	0,5355	0,8661	0,9998
	Значения мощности относительно альтернативы
0,1	0,1096	0,1107	0,1147	0,1459	0,1898	0,3265	0,6237
0,05	0,0508	0,0567	0,0563	0,0691	0,0945	0,1675	0,3986
0,025	0,0252	0,0291	0,0283	0,0334	0,0442	0,0805	0,2259
	Значения мощности относительно альтернативы
0,1	0,1655	0,2875	0,5513	0,9875	0,9999
0,05	0,0801	0,1437	0,3199	0,9470	0,9993
0,025	0,0361	0,0727	0,1687	0,8587	0,9952
	Значения мощности относительно альтернативы
0,1	0,1087	0,1069	0,1135	0,1422	0,1826	0,2978	0,5463
0,05	0,0511	0,0549	0,0581	0,0668	0,0910	0,1450	0,3390
0,025	0,0241	0,0276	0,0290	0,0332	0,0431	0,0712	0,1822

При обработке результатов измерений, в задачах статистического управления качеством обычно имеют дело с выборками достаточно ограни­ченного или, чаще, малого объема. Следует отчетливо понимать, что крите­рии однородности вследствие низкой мощности при малых объемах выборок не способны различать близкие альтернативы. Поэтому проверяемая гипо­теза об однородности выборок, даже в случае ее несправедливости, чаще не будет отклоняться. Сдвиг на или увеличение масштабного параметра (рассеяния) на 10% при малых объемах выборок критерии однородности вернее всего “не заметят”, но большие отклонения в законах, соответствую­щих выборкам, будут отмечаться. Например, для того чтобы в случае применения критерия Лемана-Розенблатта вероятности ошибок 1-го и 2-го рода не превышали 0.1 при наличии сдвига (альтернативаH1) объемы выборок должны быть порядка 2000. А при сдвиге (Альтер­натива H2) вероятно­сти ошибок не превысят величин 0.1 при объемах выборок не более 100.

Так как распределение статистики (3) очень быстро сходится к распре­делению , то использование его в качестве распределения статистики критерия Лемана-Розенблатта корректно и при малых m,n.

В случае критерия Смирнова из-за ступенчатого характера распре­деле­ния статистики (1) (особенно при n=m) использование предельного распреде­ления Колмогорова для экспериментатора будет связано с очень приблизительным знанием действительного уровня значимости (веро­ятности ошибки 1-го рода) и соответствующего критического значения. По­этому при построении процедур проверки однородности по критерию Смир­нова рекомендуется: 1) выбирать так, чтобы они представляли собой вза­имно простые числа, а их наименьшее общее кратное k было максималь­ным и равным mn; 2) использовать в критерии Смирнова статистику вида (2). Тогда применение распределения Колмогорова в качестве распределения статистики (2) критерия Смирнова будет корректным при относительно ма­лых и .

Подводя итоги и учитывая результаты сравнительного анализа мощно­сти и особенности применения, для проверки однородности целесообразно рекомендовать применение и того, и другого критерия.