Метод минимального расстояния

Равномернаяметрика, или метрика Колмогорова, - одна из наиболее старых и наиболее часто используемых вероятностных метрик. Термин «метрика Колмогорова» в отечественной литературе используется ред­ко, хотя А. Н. Колмогоров был первым, кто успешно исполь­зовал в статистике уникальные свойства Р. м., определяемой для действительных случайных величин равенством

где 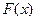- функция распределения случайной величины X. Эти свойства таковы:

1)p(G(X), G(Y)) = p(X, Y) для любой непрерывной и строго монотонной функции G{x) на ;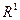

2)множество всех дискретных распределений на 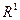являет­ся плотным (в смысле равномерной сходимости) в множестве всех распределений на .

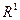Берри - Эссеена неравенство содержит верхнюю оценку Р. м. в терминах характеристических функций.

Существуют разнообразные аналоги Р.м. для распределе­ний 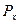многомерных случайных величин X. Обычно они имеют структуру

,

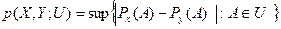где U - какая-либо система борелевских множеств. Наиболее используемыми здесь до настоящего времени были та или иная система шаров, система всех выпуклых множеств и система всех борелевских множеств. В последнем случае получается полной вариации метрика.

Суть этого метода заключается в следующем. Предположим, что любым двум функциям распределения 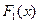и 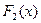поставлено в со­ответствие число

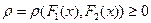,называемое расстоянием, причем 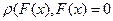. Пусть теперь, как обычно, задана выборка из генеральной совокупности с тео­ретической функцией распределения F(x), принадлежащей параметри­ческому семейству 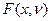. Вычислим расстояние между эмпирической функцией распределения F*(x) и функциями распределения 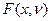из данного семейства. Оценкой, полученной методом минимального расстояния, называется такое значение 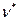, для которого

,

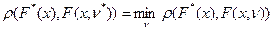т.е. такое значение 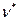, которое определяет ближайшую к F*(x) в смыс­ле расстояния 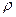функцию распределения из семейства .

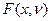Приведем примеры некоторых наиболее часто встречающихся в ма­тематической статистике расстояний.

Равномерное расстояние (расстояние Колмогорова) определяется формулой

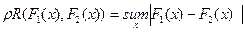
расстояние имеет вид

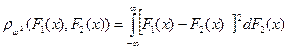
Расстояние 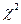употребляется для функций распределения 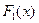и 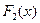дискретных случайных величин 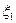и 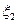, принимающих одина­ковые значения , и задается выражением

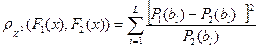
где вероятност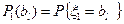и и 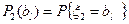определяются рядами распределения случайных величин 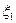и .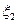

Использование приведенных выше расстояний для получения оце­нок весьма сложно в вычислительном плане, и поэтому они употребля­ются крайне редко. Здесь мы упомянули об этих расстояниях только потому, что применение оценок, полученных с их помощью, позволяет упростить вычисление уровней значимости критериев при проверке сложных непараметрических статистических гипотез, поскольку такие оценки естественным образом связаны с соответствующими критерия­ми.