Решение. 1а)Для построения области решений строим в системе координат соответствующие заданным ограничениям-неравенствам граничные прямые:

1а) Для построения области решений строим в системе координат соответствующие заданным ограничениям-неравенствам граничные прямые: , , , , 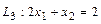, 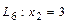. Прямая 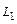проходит через точки и ; - через точк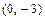и и ; - через точки и 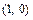; совпадает с осью ; совпадает с осью ; проходит через точку 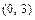параллельно оси .

2а) Находим полуплоскости 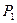, , , , и в которых выполняются неравенства. Для этого выбираем «пробную» точку и проверяем, удовлетворяет ли она ограничению-неравенству. Если удовлетворяет, то данное неравенство выполняется в полуплоскости, содержащей «пробную» точку. В противном случае берётся полуплоскость, не содержащая «пробной» точки. В качестве «пробной» точки выбирают любую точку, не принадлежащую граничной прямой, например, начало координат для нахождения полуплоскостей 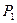, , , . Полуплоскости, в которых неравенства выполняются, отмечаем стрелками, направленными внутрь данной полуплоскости.

3а) Строим область решений как область, являющуюся пересечением полуплоскостей , отмечая её штриховкой (см. рис. 4).

Для решения задачи линейного программирования графическим способом: 1б) Строим нормальный вектор прямой , являющейся линией уровня целевой функции . (вектор 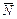показывает направление возрастания значений целевой функции).

2б) Перпендикулярно вектору проводим пунктиром линию уровня .

3б) Параллельным перемещением линии уровня находим крайние точки области допустимых решений , в которых целевая функция достигает минимума – точку 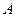и максимума – точку .

4б) Определяем координаты точек 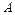и . Точку (точк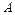а пересечения прямых и ) находим решая систему уравнений . Откуда . Точку (точка пересечения прямых 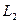и ) находим решая систему уравнений . Откуда .

5б) Вычисляем:

и .

Рис. 4

Ответ: а) Область (см. рис.4)

б) ; .