 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Краткие теоретические сведения. 3 страница
|
|
Всякий геометрический вектор может быть разложен единственным образом по векторам базиса, коэффициенты разложения называются при этом координатами вектора в данном базисе. Например, если  - базис
- базис 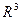 и
и  , то всегда существует единственное разложение:
, то всегда существует единственное разложение:  , где числа
, где числа  - координаты вектора
- координаты вектора 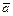 в базисе
в базисе  , при этом пишут
, при этом пишут 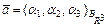 . Если в
. Если в  зафиксирован ортонормированный базис
зафиксирован ортонормированный базис  и
и  , то равносильны записи:
, то равносильны записи:  и
и 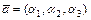 (в записи вектора в координатной форме ортонормированный базис не указывают).
(в записи вектора в координатной форме ортонормированный базис не указывают).
Представление геометрических векторов в координатной форме, позволяет выполнять действия над ними, как над арифметическими векторами:
 ;
;
 .
.
Декартовой прямоугольной системой координатв пространстве называется совокупность точки  (начало координат) и правого ортонормированного базиса
(начало координат) и правого ортонормированного базиса  и обозначается
и обозначается 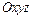 . Прямые
. Прямые  ,
,  ,
,  , проходящие через начало координат в направлении базисных векторов, называются координатными осями: первая – осью абсцисс, вторая – осью ординат, третья – осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Аналогично вводится система координат на плоскости:
, проходящие через начало координат в направлении базисных векторов, называются координатными осями: первая – осью абсцисс, вторая – осью ординат, третья – осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями. Аналогично вводится система координат на плоскости:  .
.
Пусть  - произвольная точка пространства, в котором введена система координат
- произвольная точка пространства, в котором введена система координат  =
= 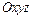 . Радиус-вектором точки
. Радиус-вектором точки  называется вектор
называется вектор  , который всегда единственным образом можно представить в виде:
, который всегда единственным образом можно представить в виде: 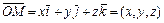 . Числа
. Числа  , являющиеся координатами радиус-вектора, совпадают с проекциями вектора
, являющиеся координатами радиус-вектора, совпадают с проекциями вектора  на базисные орты
на базисные орты  и
и 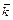 (на координатные оси
(на координатные оси  и
и  ). Координатами точки
). Координатами точки  в системе координат
в системе координат  называются координаты её радиус-вектора
называются координаты её радиус-вектора  и пишут
и пишут  . В свою очередь, координаты точки
. В свою очередь, координаты точки  полностью определяют её радиус-вектор
полностью определяют её радиус-вектор 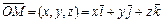 . Всякий геометрический вектор
. Всякий геометрический вектор  в системе координат
в системе координат  , всегда можно представить как радиус-вектор некоторой точки и записать в виде:
, всегда можно представить как радиус-вектор некоторой точки и записать в виде:  .
.
Длина 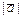 вектора
вектора 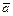 , заданного координатами
, заданного координатами  , определяется формулой:
, определяется формулой:  . Направляющими косинусами вектора
. Направляющими косинусами вектора 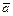 называются числа:
называются числа:  ,
,  ,
,  , при этом
, при этом  .
.
Координаты вектора  , заданного точками
, заданного точками 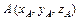 и
и  определяются по формуле:
определяются по формуле:  . Расстояние
. Расстояние  между точками
между точками  и
и  определяется как длина вектора
определяется как длина вектора  и находится по формуле:
и находится по формуле:
 .
.
Координаты точки  делящей отрезок
делящей отрезок  пополам находятся по формулам:
пополам находятся по формулам:  ,
,  ,
,  .
.
Скалярным произведением векторов 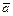 и
и 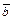 называется число
называется число  . Скалярное произведение обладает свойствами:
. Скалярное произведение обладает свойствами:
1)  ; 2)
; 2)  где
где 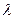 - число;
- число;
3) 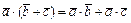 ; 4)
; 4) 
5)  ; 6)
; 6)  ,
,  ,
, 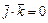 ,
,  ,
,  ,
,  . Для векторов
. Для векторов 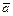 и
и 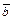 , заданных своими координатами
, заданных своими координатами  ,
,  скалярное произведение вычисляется по формуле:
скалярное произведение вычисляется по формуле:  .
.
Скалярное произведение применяют: 1) для вычисления угла между векторами 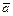 и
и 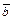 по формуле:
по формуле:  ; 2) для вычисления проекции вектора
; 2) для вычисления проекции вектора 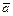 на вектор
на вектор 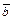 по формуле:
по формуле:  ; 3) для вычисления длины вектора
; 3) для вычисления длины вектора  по формуле:
по формуле:  ; 4) в качестве условия перпендикулярности векторов
; 4) в качестве условия перпендикулярности векторов 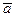 и
и  :
:  .
.
Векторным произведением векторов 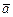 и
и 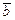 называется вектор
называется вектор  , определяемый условиями: 1)
, определяемый условиями: 1) 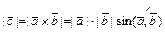 ;
;
2)  и
и  ; 3)
; 3)  - правая тройка векторов.
- правая тройка векторов.
Упорядоченная тройка  некомпланарных векторов называется правой тройкой, если из конца третьего вектора
некомпланарных векторов называется правой тройкой, если из конца третьего вектора 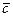 , кратчайший поворот от первого вектора
, кратчайший поворот от первого вектора 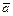 ко второму
ко второму 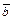 , виден совершающимся против хода часовой стрелки. В противном случае, тройка
, виден совершающимся против хода часовой стрелки. В противном случае, тройка  называется левой.
называется левой.
Векторное произведение обладает свойствами:
1)  ; 2)
; 2) 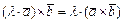 , где
, где 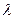 - число;
- число;
3) 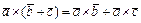 ; 4)
; 4)  5)
5)  ;
;
6)  ,
, 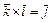 ,
,  ,
,  ,
,  ,
,  .
.
Для векторов 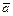 и
и 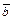 , заданных своими координатами
, заданных своими координатами  ,
,  векторное произведение вычисляется по формуле:
векторное произведение вычисляется по формуле:  .
.
Векторное произведение 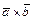 применяют: 1) для вычисления площадей треугольника и параллелограмма, построенных на векторах
применяют: 1) для вычисления площадей треугольника и параллелограмма, построенных на векторах 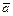 и
и 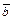 , как на сторонах, по формуле:
, как на сторонах, по формуле:  ; 2) в качестве условия параллельности векторов
; 2) в качестве условия параллельности векторов 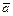 и
и 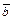 :
:  .
.
Смешанным произведением упорядоченной тройки векторов 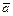 ,
, 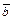 и
и  называется число
называется число  .
.
Смешанное произведение обладает свойствами:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  и
и 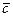 -компланарны
-компланарны  ;
;
5)  , где
, где  -объём параллелепипеда, построенного на векторах
-объём параллелепипеда, построенного на векторах 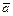 ,
, 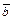 и
и  .
.
Для векторов 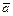 ,
, 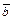 и
и  , заданных своими координатами
, заданных своими координатами  ,
,  ,
,  смешанное произведение вычисляется по формуле:
смешанное произведение вычисляется по формуле:  .
.
Смешанное произведение 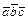 применяют: 1) для вычисления объёмов тетраэдра и параллелепипеда, построенных на векторах
применяют: 1) для вычисления объёмов тетраэдра и параллелепипеда, построенных на векторах 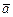 ,
, 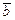 и
и  , как на рёбрах, по формуле:
, как на рёбрах, по формуле:  ; 2) в качестве условия компланарности векторов
; 2) в качестве условия компланарности векторов 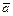 ,
, 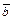 и
и  :
:  и
и 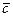 - компланарны.
- компланарны.
Тема 8. Прямые линии и плоскости.
Нормальным вектором прямой  , называется всякий ненулевой вектор
, называется всякий ненулевой вектор 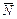 перпендикулярный данной прямой. Направляющим вектором прямой
перпендикулярный данной прямой. Направляющим вектором прямой  , называется всякий ненулевой вектор
, называется всякий ненулевой вектор  параллельный данной прямой.
параллельный данной прямой.
Прямая  на плоскости в системе координат
на плоскости в системе координат 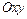 может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение прямой, где
- общее уравнение прямой, где  - нормальный вектор прямой;
- нормальный вектор прямой;
2) 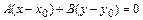 - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку  перпендикулярно данному вектору
перпендикулярно данному вектору  ;
;
3)  - уравнение прямой, проходящей через точку
- уравнение прямой, проходящей через точку  параллельно данному вектору
параллельно данному вектору  (каноническое уравнение);
(каноническое уравнение);
4)  - уравнение прямой, проходящей через две данные точки
- уравнение прямой, проходящей через две данные точки  ,
,  ;
;
5)  -уравнения прямой с угловым коэффициентом
-уравнения прямой с угловым коэффициентом 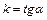 , где
, где  - точка через которую прямая проходит;
- точка через которую прямая проходит; 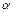 (
( ) – угол, который прямая составляет с осью
) – угол, который прямая составляет с осью  ;
;  - длина отрезка (со знаком
- длина отрезка (со знаком  ), отсекаемого прямой на оси
), отсекаемого прямой на оси  (знак «
(знак « », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « », если на отрицательной).
», если на отрицательной).
6)  -уравнение прямой в отрезках, где
-уравнение прямой в отрезках, где  и
и  - длины отрезков (со знаком
- длины отрезков (со знаком  ), отсекаемых прямой на координатных осях
), отсекаемых прямой на координатных осях  и
и  (знак «
(знак « », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « », если на отрицательной).
», если на отрицательной).
Расстояние от точки  до прямой
до прямой  , заданной общим уравнением
, заданной общим уравнением  на плоскости, находится по формуле:
на плоскости, находится по формуле:
 .
.
Угол  , (
, ( ) между прямыми
) между прямыми  и
и  , заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:
, заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:
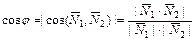 ;
;  .
.
 , если
, если 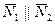
 или
или  .
.
 ,если
,если  или
или 
Координаты точки пересечения прямых  и
и  находятся как решение системы линейных уравнений:
находятся как решение системы линейных уравнений: 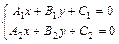 или
или  .
.
Нормальным вектором плоскости  , называется всякий ненулевой вектор
, называется всякий ненулевой вектор 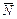 перпендикулярный данной плоскости.
перпендикулярный данной плоскости.
Плоскость  в системе координат
в системе координат  может быть задана уравнением одного из следующих видов:
может быть задана уравнением одного из следующих видов:
1)  - общее уравнение плоскости, где
- общее уравнение плоскости, где  - нормальный вектор плоскости;
- нормальный вектор плоскости;
2)  - уравнение плоскости, проходящей через точку
- уравнение плоскости, проходящей через точку  перпендикулярно данному вектору
перпендикулярно данному вектору  ;
;
3)  - уравнение плоскости, проходящей через три точки
- уравнение плоскости, проходящей через три точки 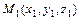 ,
, 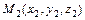 и
и  ;
;
4)  -уравнение плоскости в отрезках, где
-уравнение плоскости в отрезках, где  ,
,  и
и  - дины отрезков (со знаком
- дины отрезков (со знаком  ), отсекаемых плоскостью на координатных осях
), отсекаемых плоскостью на координатных осях  ,
,  и
и  (знак «
(знак « », если отрезок отсекается на положительной части оси и «
», если отрезок отсекается на положительной части оси и « », если на отрицательной).
», если на отрицательной).
Расстояние от точки  до плоскости
до плоскости  , заданной общим уравнением
, заданной общим уравнением  , находится по формуле:
, находится по формуле:
 .
.
Угол  , (
, ( ) между плоскостями
) между плоскостями  и
и  , заданными общими уравнениями, находится по формуле:
, заданными общими уравнениями, находится по формуле:
Дата публикования: 2014-11-18; Прочитано: 291 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
