 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приложения. Образец решения контрольных задач типового варианта
|
|
Образец решения контрольных задач типового варианта.
1 – 10. Вычислить определитель: 

а) непосредственным разложением по  строке;
строке;
б) непосредственным разложением по  столбцу;
столбцу;
Решение. а) вычисляем определитель разложением по элементам первой строки: 
 =
=  .
.






Тогда  =
=  =
= 
б) вычисляем определитель непосредственным разложением по элементам второго столбца: 
 =
=  .
.






Тогда  =
=  =
=  .
.
Ответ: 
 .
.
11-20. Найти матрицу  , если:
, если:
 ,
, 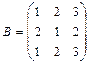 .
.
Решение:
1) Транспонируем матрицу 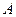 :
:  .
.
2) Вычисляем произведение матриц  :
:


 .
.
3) Находим матрицу  :
:
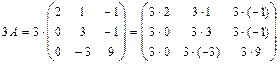
 .
.
4) Находим матрицу  :
: 

 .
.
Ответ:  .
.
21-30. Найти собственные числа и векторы матрицы  .
.
Множество собственных чисел матрицы совпадает с множеством корней характеристического уравнения матрицы 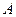 :
:  , а множество собственных векторов, отвечающих собственному числу
, а множество собственных векторов, отвечающих собственному числу  , совпадает с множеством ненулевых решений матричного уравнения:
, совпадает с множеством ненулевых решений матричного уравнения:  , определяемым методом Гаусса.
, определяемым методом Гаусса.
Решение:
1) Составляем характеристическое уравнение матрицы 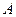 :
:
 .
.
Записываем его в виде алгебраического уравнения и находим действительные корни (среди них могут быть и кратные):

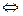


 ,
,  .
.
Таким образом, собственными числами матрицы 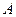 являются:
являются:  и
и  .
.
2) Находим собственные векторы матрицы 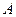 , отвечающие различным собственным числам
, отвечающие различным собственным числам  и
и  .
.
2.1) Составляем матричное уравнениедля нахождения собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  :
: 
или

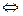
 ,
,
записываем его в виде системы линейных уравнений:  и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе  , имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной
, имеющей специальный (трапециевидный) вид. Такая система имеет бесконечно много решений, которые записывают в виде общего решения. Для записи общего решения этой системы указываем её базисные и свободные неизвестные. Базисными являются неизвестные, столбцы коэффициентов системы при которых образуют базисный минор матрицы этой системы. Такой минор образует, например, столбец коэффициентов при неизвестной  :
:  . Поэтому выбираем в качестве базисной – неизвестную
. Поэтому выбираем в качестве базисной – неизвестную  , тогда свободными будут неизвестные
, тогда свободными будут неизвестные 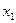 и
и 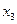 . Свободным неизвестным придаём разные, произвольные постоянные значения:
. Свободным неизвестным придаём разные, произвольные постоянные значения:  ,
, 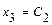 , где
, где  ,
, 
 , одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:
, одновременно, и выражаем через них значение базисной неизвестной из уравнения системы:  . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  будет иметь вид:
будет иметь вид:  .
.
2.2) Составляем матричное уравнениедля нахождения собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  :
: 
или

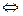
 ,
,
записываем его в виде системы линейных уравнений:  и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе
и решаем методом Гаусса. Полученная система, очевидно, эквивалентна системе  , имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных
, имеющей специальный (трапециевидный) вид. Система имеет бесконечно много решений. Для записи её общего решения указываем базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных 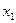 и
и  :
:  . Поэтому выбираем в качестве базисных – неизвестные
. Поэтому выбираем в качестве базисных – неизвестные 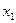 и
и  , тогда свободной будет неизвестная
, тогда свободной будет неизвестная 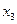 . Свободной неизвестной придаём произвольное постоянное значение:
. Свободной неизвестной придаём произвольное постоянное значение:  , где
, где  и выражаем через неё значения базисных неизвестных
и выражаем через неё значения базисных неизвестных 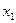 и
и  из уравнений системы специального (трапециевидного) вида, начиная с последнего уравнения:
из уравнений системы специального (трапециевидного) вида, начиная с последнего уравнения: 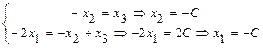 . Тогда общее решение системы, задающее множество всех собственных векторов
. Тогда общее решение системы, задающее множество всех собственных векторов  , отвечающих собственному числу
, отвечающих собственному числу  , будет иметь вид:
, будет иметь вид:  ,
,  .
.
Ответ:  ,
,  ,
,  ,
, 
 ;
;
 ,
,  ,
,  .
.
31 – 40. Дана система уравнений:  . Требуется:
. Требуется:
а) найти решение системы методом Крамера; б) записать систему в матричном виде и найти её решение методом обратной матрицы; в) найти решение системы методом Гаусса.
Дата публикования: 2014-11-18; Прочитано: 286 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
