 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
III. Мішаний добуток
|
|
1. Поняття мішаного добутку
Означення 1. Мішаним добутком трьох векторів 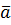 ,
, 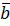 ,
, 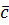 називається скалярний добуток двох векторів векторного добутку
називається скалярний добуток двох векторів векторного добутку 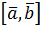 і вектора
і вектора 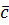 :
: 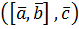 .
.
2. Геометричні та алгебраїчні властивості.
Теорема 1 (про геометричний зміст мішаного добутку). Мішаний добуток векторів 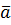 ,
, 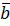 ,
, 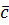 дорівнює об’єму паралелепіпеда, побудованого на векторах
дорівнює об’єму паралелепіпеда, побудованого на векторах 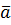 ,
, 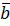 ,
, 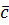 , зведених до спільного початку, зі знаком (+), якщо трійка векторів
, зведених до спільного початку, зі знаком (+), якщо трійка векторів 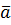 ,
, 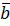 ,
, 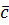 – права, і зі знаком (-), якщо вона ліва.
– права, і зі знаком (-), якщо вона ліва.
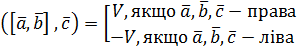
Доведення (навести доведення).
З цієї теореми можна отримати наслідок.
Наслідок. Для того щоб три вектори 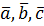 були компланарними необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю.
були компланарними необхідно і достатньо, щоб їх мішаний добуток дорівнював нулю.
Наслідком теореми 1 є також така алгебраїчна властивість
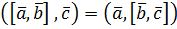
(Навести доведення цієї властивості).
Оскільки з доведеної рівності виходить, що квадратні дужки можна поставити будь-як, то домовились позначати мішаний добуток так 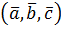 .
.
Що стосується інших алгебраїчних властивостей, то є наслідками скалярного і векторного добутку.
Наприклад, можна довести, що 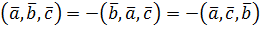
(Навести доведення)
3. Вираз мішаного добутку через координати векторів.
Нехай в ортонормованому базисі  вектори
вектори 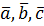 мають такі розкладання:
мають такі розкладання:
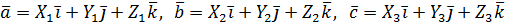 .
.
Треба знайти вираз 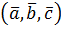 через координати векторів.
через координати векторів.
Користуючись властивостями скалярного і мішаного добутків, можна довести таку формулу:
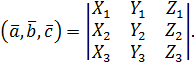
Дата публикования: 2014-11-18; Прочитано: 759 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
