 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
I. Скалярний добуток
|
|
1. Скалярна проекція вектора на вісь.
Почнемо з допоміжного поняття величини напрямленого відрізку.
Розглянемо вісь u і напрямлені відрізки на осі u.
Означення 1. Величиною напрямленого відрізку 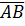 називається число, що позначається
називається число, що позначається 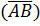 :
:
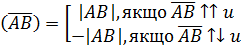
Розглянемо тепер вектори, що не обов’язково належать осі u.
| B |
| A |
Означення 2. Векторною проекцією вектора AB на вісь u називається вектор 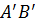 , де
, де 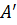 ортогональна проекція точки A,
ортогональна проекція точки A, 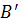 – отрогональна проекція точки B.
– отрогональна проекція точки B.
Позначимо векторну проекцію
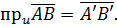
Означення 3. Скалярною проекцією 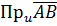 вектора
вектора 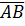 на вісь u називається величина його векторної проекції
на вісь u називається величина його векторної проекції
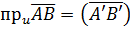 .
.
Теорема 1. Скалярна проекція вектора на вісь дорівнює добутку довжини цього вектора на косинус кута між вектором та віссю.
Доведення. (навести доведення)
Для доведення властивостей скалярних проекцій векторів корисною є теорема про геометричний зміст декартових прямокутних координат.
Теорема 2. Декартові прямокутні координати є проекціями вектора на відповідні координатні осі.
Скалярна проекція має такі властивості.
Теорема 3. Скалярна проекція суми двох векторів дорівнює сумі скалярних проекцій цих векторів
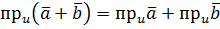 .
.
Доведення. (навести доведення)
Теорема 4. Скалярна проекція добутку вектора на число дорівнює добутку цього числа на скалярну проекцію вектора
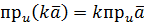 .
.
2. Поняття скалярного добутку.
Означення 3. Скалярним добутком двох векторів 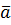 і
і 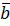 називається число
називається число  , що дорівнює добутку довжин цих векторів на косинус кута між ними.
, що дорівнює добутку довжин цих векторів на косинус кута між ними.

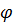
|
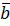
|
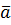
|
Останню рівність можна записати у вигляді
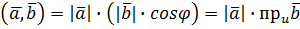
або
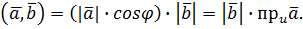
Звідси випливає інше означення скалярного добутку.
Означення 4. Скалярним добутком векторів 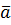 та
та 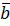 називається добуток довжини одного з векторів на скалярну проекцію другого вектора на напрямок першого.
називається добуток довжини одного з векторів на скалярну проекцію другого вектора на напрямок першого.
3. Алгебраїчні та геометричні властивості скалярного добутку
Доведемо, що скалярний добуток має такі алгебраїчні властивості:
1) 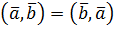 (властивість симетрії)
(властивість симетрії)
2) 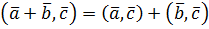 (дистрибутивність)
(дистрибутивність)
3) 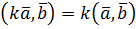
4) 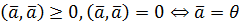
(навести доведення перелічених властивостей).
Зауваження. З властивостей 3) та 1) випливає, що 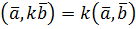 .
.
Зі скалярним добутком пов’язана така геометрична властивість:
Для того щоб вектори були ортогональними (перпендикулярними) необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю (навести доведення необхідності і достатності умови).
4. Вираз скалярного добутку через координати векторів
Означення. Базис простору (площини) називається ортонормованим, якщо він складається з попарно ортогональних векторів, довжина яких дорівнює одиниці.
Нехай в просторі введено ортонормований базис  , тобто
, тобто 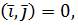
 нехай далі вектори
нехай далі вектори 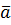 і
і 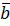 мають координати
мають координати 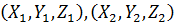 , відповідно.
, відповідно.
Теорема. Скалярний добуток 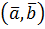 в ортонормованому базисі дорівнює сумі добутків відповідних координат векторів
в ортонормованому базисі дорівнює сумі добутків відповідних координат векторів 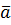 і
і 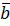 , тобто
, тобто
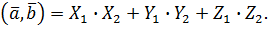
Доведення. (навести доведення)
З означення скалярного добутку і отриманої формули випливає:
1) 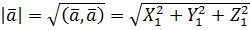
2) 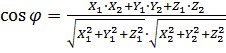
Дата публикования: 2014-11-18; Прочитано: 1757 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
