Закона парности касательных напряжений

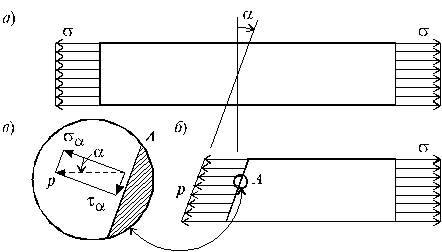Чистым сдвигом называют такой вид нагруженного состояния, при котором по граням выделенного из материала элемента действуют только касательные напряжения.

Напряжение на наклонных площадках

Из условия åz = 0, записанного для отсеченной части стержня получим: р Fa = s F (*), где F - площадь поперечного сечения стержня, Fa = F/cos a - пло­щадь наклонного сечения. Из (*) легко установить: р = s сos a. (**) Раскладывая напряжение р по нормали и касательной к на­клонной площадке с учетом (**) получим: sa = p cos a = s cos2 a; ta = p sin a = 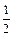s sin 2 a. (***)

Для одной и той же точки тела величина напряжений, возникающих в сечениях, проходящих через эту точку, зависит от ориентации этой площадки, т.е. от угла a. При a = 0 из (***) следует, что sa = s, ta = 0. При a = 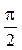, т.е. на продольных площадках, sa = ta = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения ta принимают наибольшие зна­чения при a = 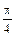, и их величина составляет tmax= . Важно отме­тить, как это следует что 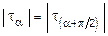. Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название закона парности касательных напряжений