 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вопрос № 1. Вывод формул для определения напряжений и перемещений при растяжении(сжатии) прямого стержня
|
|
Под растяжением (сжатием) понимают такой вид нагружения, при котором в поперечных сечениях возникает только нормальные силы, а прочие силовые факторы равны нулю.
В соответствии с гипотизой плоских сечений: плоские сечения до деформации остаются плоскими и после деформации. Значит, все продольные волокна стержня находятся в одинаковых условиях, а следовательно, нормальные напряжения во всех точках поперечного сечения должны быть одинаковы и равны 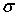 = Nz /А, где А – площадь поперечного сечения стержня.
= Nz /А, где А – площадь поперечного сечения стержня.
Определим упругие деформации стержня, предполагая что изменения его длины при растяжении 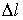 , называемое абсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной. Тогда относительная продольная деформация будет равна
, называемое абсолютной продольной деформацией или удлинением, мало по сравнению с его первоначальной длиной. Тогда относительная продольная деформация будет равна 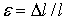
Согласно закону Гука: 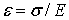 , где Е – модуль продольной упругости, отсюда следует, что,
, где Е – модуль продольной упругости, отсюда следует, что,
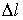 = Nz / EA, где EА – жесткость поперечного сечения стержня при распределении (сжатии).
= Nz / EA, где EА – жесткость поперечного сечения стержня при распределении (сжатии).
Эта формула применяется только в случае, когда по длине стержня ни жескость поперечного сечения, ни продольная сила не изменяется. В случае, когда Nz и EА меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах частей длиной dz, получаем: 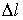 =
= 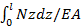
Дата публикования: 2014-11-18; Прочитано: 1202 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
