 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ряды аналитических функций
|
|
1. Понятие функционального ряда.
Пусть дана последовательность { u k(z)} функций, z Î g. Выражение  - называется функциональным рядом, заданным в g.
- называется функциональным рядом, заданным в g.
Определение. Если при " z Î g, соответствующий числовой ряд сходится к определенному комплексному числу f(z), то в g определена функция, которая называется суммой функционального ряда, а сам ряд называется сходящимся в g.
rn (z)= f(z)-  - n-ый остаток ряда
- n-ый остаток ряда
Если ряд сходится в g, то
"e>0 $ N(e,z): | r n(z)| <e для " n > N (e, z).
Пример.
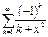 - знакочередующийся ряд, сходится и признаку Лейбница, остаток ряда не превышает модуля следующего слагаемого
- знакочередующийся ряд, сходится и признаку Лейбница, остаток ряда не превышает модуля следующего слагаемого

Необходимый и достаточный признак сходимости:
Критерий Коши: для "e>0 $ N(e,z): | Sn+m(z)-Sn(z)| <e для "n > N и "m>0.
Вообще говоря, в каждой точке z Î g N свое: N=N(e,z) и общего N для всей z может и не существовать.
2. Равномерная сходимость å uk (z) в области g.
Определение. Если для "e>0 $ N(e): | rn(z)| <e для "n >N(e) и " z одновременно, то ряд å uk(z) называется равномерно сходящимся к функции f(z) в g.
Обозначение: å uk(z)=>f(z).
Критерий Коши (необходимое и достаточное условие равномерной сходимости).
Если для "e>0 $ N(e): | Sn+m(z)-Sn(z)| <e для "n > N и "m>0 и " z одновременно, то ряд å uk(z)=>f(z).
Доказательство.
Необходимость.
Пусть å uk(z)=>f(z) "e >0 $ N(e): | f(z)- Sn(z)| <e /2 для "n>N(e) и " z Îg => и | f(z)- Sn+m(z)| <e /2 =>
=>| Sn+m(z)-Sn(z)| <e для "n>N и "m>0 и "zÎg.
Достаточность. Пусть для "e>0 $ N(e): | Sn+m(z)-Sn(z)| <e для "n>N и "m>0 и "zÎg =>  сходится в " z Îg, т.о. в g определена f(z) =
сходится в " z Îg, т.о. в g определена f(z) =  .
.

для "n>N(e) и "zÎg => | rn(z)| <e для "n>N(e) и " z Îg. n
Признак Вейерштрасса (достаточный признак равномерной сходимости).
Если | uk(z) |< ak, ak >0 для " k >N и " z Îg и S ak сходится, то S uk(z)=>f(z) в g.
Доказательство.
S ak сходится => "e>0 $ N(e):  <e для "n>N(e)
<e для "n>N(e)

для "n>N(e) и "zÎg. n
Примеры.

 (оценить сверху значением функции в ее максимуме)
(оценить сверху значением функции в ее максимуме)
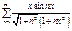 (оценить сверху значением функции
(оценить сверху значением функции  в ее максимуме
в ее максимуме  )
)
 (
( )
)
3. Свойства равномерно сходящихся рядов.
Свойства равномерно сходящихся рядов:
Теорема 14.1. (непрерывность суммы) Пусть uk(z) ÎС(g) и S uk(z)=>f(z), тогда f(z) ÎС(g).
Доказательство.
uk(z)=>f(z) Þ одновременно выполнены неравенства
| f (z +D z)-Sn(z +D z)|< e/3 и | f (z)-Sn(z)|< e/3 для "e>0.
uk(z) ÎС(g) Þ для "e>0 и "N $ d>0:

при |D z |<d
Þ |D f |=| f (z +D z)- f (z)|£
£| f (z +D z)-Sn(z +D z)|+|Sn(z +D z)-Sn(z)|+|Sn(z)- f(z) | £
£e/3+e/3+e/3=e для |D z |<d, n>N. n
Примеры
 Ряд из непрерывных функций сходится к разрывной функции, значит сходимость неравномерная
Ряд из непрерывных функций сходится к разрывной функции, значит сходимость неравномерная
 аналогично
аналогично
Теорема 14.2. (возможность почленного интегрирования). Пусть uk (z)ÎС(g) и S uk(z)=>f(z), G кусочно- гладкий контур GÌg конечной длины L. Тогда  .
.
Доказательство
uk(z)=>f(z) Þ
для "e>0 $ N(e): | rn(z) |<e/L для "n>N(e)
 =
=  £
£  <
<  =en
=en
Замечание. Эти два свойства равномерно сходящихся рядов с комплексными членами совершенно аналогичны свойствам равномерно сходящихся функциональных рядов с действительными членами.
Примеры.
Найти  , если
, если 
Является ли непрерывной функция 



Теорема Вейерштрасса. Если uk(z) ÎC¥(g) и S uk(z)=>f(z) в любой  замкнутой подобласти области g то:
замкнутой подобласти области g то:
f (z)ÎC¥(g).
 , для " z Îg.
, для " z Îg.
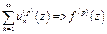 " z Î"
" z Î"  .
.
Доказательство
1. Рассмотрим произвольную z 0Îg и построим односвязную  : z 0Î
: z 0Î  , в силу Теоремы 14.1 f (z)ÎС(g).
, в силу Теоремы 14.1 f (z)ÎС(g).
Рассмотрим произвольный контур GÌ  . По Теореме 14.2
. По Теореме 14.2  .
.
Т.о. для f(z) выполнены все условия Теоремы Морера Þ f (z)ÎC¥( ). В силу произвольности
). В силу произвольности  f (z)ÎC¥(g).
f (z)ÎC¥(g).
Замечание. Т.к. rn (z) =f (z)-Sn(z) Þ rn (z) ÎC¥(g).
2. Рассмотрим произвольную z 0Îg и произвольный контур GÌg. Обозначим  .
.
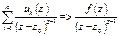 для " zÎG, т.к.
для " zÎG, т.к. 
По Теореме 14.2 это равенство можно проинтегрировать почленно
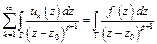
По Теореме 8.1.
 .
.
В силу произвольности z0 утверждение 2 доказано.
Замечание. rn(p)(z)=f(p)(z)-Sn (p)(z)=  .
.
3. Рассмотрим "  и G - замкнутый контур:
и G - замкнутый контур:  ÌGÌgи "zÎ
ÌGÌgи "zÎ  и "xÎG | z -x|³d>0.
и "xÎG | z -x|³d>0.
rn (z) ÎC¥(g) Þ  для "zÎ
для "zÎ  .
.
uk(z)=>f(z) Þ "e>0 $ N(e):  , где L- длина G.
, где L- длина G.
Тогда  .
.
Т.о. получена равномерная оценка для остатка ряда для производных Þ 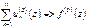 .
.
Пример. Ряд Szk/k2 сходится равномерно в круге |z|£1, а ряд из производных Szk-1/k не может равномерно сходится в этом круг, т.к. он расходится при z=1. Ряд Szk-1/k равномерно сходится при |z|<1.
Для равномерно сходящихся функциональных рядов с действительными членами верна
Теорема 14.3. Пусть uk(x) – непрерывно дифференцируемы на отрезке [ a,b ] и ряд, составленный из производных  - равномерно сходится на отрезке [ a,b ], тогда если ряд
- равномерно сходится на отрезке [ a,b ], тогда если ряд  сходится хотя бы в одной точке c Î[ a,b ], то он равномерно сходится на всем отрезке [ a,b ], его сумма
сходится хотя бы в одной точке c Î[ a,b ], то он равномерно сходится на всем отрезке [ a,b ], его сумма  непрерывно дифференцируема и
непрерывно дифференцируема и  .
.
Доказательство.
Пусть  (непрерывна в силу равномерной сходимости ряда).
(непрерывна в силу равномерной сходимости ряда).
Найдем первообразную
 для
для  . Ряд
. Ряд  сходится по условию теоремы Þ
сходится по условию теоремы Þ  тоже сходится на всем промежутке.
тоже сходится на всем промежутке.

Левая часть равенства имеет производную по x Þ$ S ¢(x)=s(x) и
 сходится равномерно, т.к. первый ряд справа сходится равномерно, а второй не зависит от x.
сходится равномерно, т.к. первый ряд справа сходится равномерно, а второй не зависит от x.
Примеры.
Равномерно сходящийся на всей действительной оси ряд  дифференцировать нельзя, так как ряд из производных
дифференцировать нельзя, так как ряд из производных  расходится, например при x =0.
расходится, например при x =0.
(1+1+1+1+…)¢=0+0+0+0+… Ряд, полученный в результате формального дифференцирования, сходится и даже равномерно, но дифференцирование не правомерно, т.к. исходный ряд расходится.
 почленное дифференцирование возможно в силу равномерной сходимости ряда из производных.
почленное дифференцирование возможно в силу равномерной сходимости ряда из производных.
§15. Степенные ряды.
Определение. Степенным рядом назовем ряд вида cn (z-z 0) n, z 0 -центр, cn - коэффициенты - заданные комплексные числа. При z= z 0 ряд очевидно сходится. Это может быть единственная точка сходимости S n!zn, а также ряд может сходится на всей комплексной плоскости S zn / n!. При исследовании степенного ряда важно установить область его равномерной сходимости. Как будет показано далее, область сходимости степенного ряда определяется видом его коэффициентов cn.
Дата публикования: 2014-11-18; Прочитано: 605 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
