 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Формула Грассмана
|
|
Теория множеств используется при решении задач следующего вида:
В группе зверей 15 умных, 13 – красивых, и 8 мартышек. Сколько зверей в группе?
Решение:
Пусть U – множество умных зверей, К – множество красивых. Тогда множество мартышек будет обозначаться как 
, а множество всех зверей – 
. Значит, | U| = 15, |K| = 13 и 
= 8. Требуется найти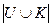 
. Так как мартышки входят как в множество умных, так и в множество красивых, то при простом сложении элементов множеств, мы мартышек посчитаем два раза. Тогда из суммы элементов множеств умных и красивых нужно одну часть мартышек вычесть. Получим формулу: 
. Эта формула носит название формулы Грассмана для двух множеств. С помощью этой формулы найдем количество зверей: 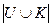= 15 + 13 – 8 = 20.
Пример 5. В классе 35 учеников. 20 человек посещают математический кружок, 11 – биологический. 10 человек не посещают кружков. Сколько биологов увлекается математикой?
Решение:
Изобразим ситуацию, изложенную в задаче, с помощью кругов Эйлера:
Тогда |E| = 35, |A| = 20, |B| = 11, |E\(A È B)| = 10. Требуется найти, чему равно | A Ç B|. Сначала найдем, чему равно | A È B|. | A È B| = |E| – |E\(A È B)| = 35 – 10 = 25. Теперь подставим известные значения в формулу Грассмана:
25 = 20 + 11 - |A Ç B|. Выразим из этого уравнения | A Ç B| и найдем, чему оно равно: | A Ç B| = 20 + 11 – 25 = 31 – 25 = 6. Таким образом, 6 учеников увлекаются и биологией, и математикой.
Контрольные вопросы
1 Назовите основателя теории множеств.
2 Дайте определение множества, элемента множества.
3 Какие способы задания множеств вы знаете?
4 Какие множества называют равными?
5 Дайте определение подмножества. Чем отличаются собственные подмножества от несобственных?
6 Какие множества называются числовыми? Приведите примеры числовых множеств.
7 Пересечение, и объединение множеств. Примеры.
8 Вычитание и дополнение множеств. Примеры.
9 Какая из операций сильнее (выполняется раньше)?
10 Как изображаются операции над множествами с помощью диаграмм Эйлера-Венна?
11 Перечислите свойства операций над множествами.
12 Для решения каких задач используют формулу Грассмана?
Тема3: Элементы математической логики
…Встреча математики с логикой в прошлом столетии привела к таким же последствиям, что и приход принца в зачарованный замок спящей красавицы: после столетий глубокого сна логика вновь расцвела плодотворной жизнью.
Дата публикования: 2014-11-18; Прочитано: 2222 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
