 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пересечение множеств
|
|
Рассмотрим два множества: Х = {0, 1, 3, 5}, Y = {1, 2, 3, 4}.
Числа 1 и 3 и только они принадлежат одновременно обоим множествам Х и Y. Составленное из них множество {1, 3} содержит все общие для множеств Х и Y элементы.
Множество, состоящее из всех элементов, принадлежащих и множеству А, и множеству В, называется пересечением множеств А и В и обозначается А ∩ В. А ∩ В = {х 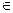 А и х
А и х 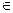 В}.
В}.
Таким образом, множество {1, 3} является пересечением рассмотренных множеств Х и Y: {0, 1, 3, 5} ∩ {1, 2, 3, 4} = {1, 3}.
В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А ∩ В = Ø.
Пересечение любого множества А с пустым множеством есть пустое множество: А ∩ Ø = Ø.
Алгебраические операции над множествами и их свойства излагаются обычно с применением кругов Эйлера или диаграмм Венна (или диаграмм Эйлера-Венна).
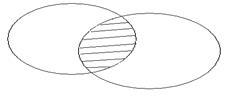 Пересечением множеств А и В, у которых есть общие элементы, будет заштрихованная область.
Пересечением множеств А и В, у которых есть общие элементы, будет заштрихованная область.
А ∩ В
Если множества не имеют общих элементов, то их пересечение будет выглядеть так:



Если одно из множеств является подмножеством другого, то их пересечение будет выглядеть так:


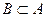
Дата публикования: 2014-11-18; Прочитано: 1521 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
