 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычитание множеств
|
|
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Разностью множеств А и В называется множество, содержащее все элементы, которые принадлежат множеству А и не принадлежат множеству В, обозначается А \ В. А \ В = { х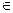 
А и х 
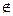В }.
Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Если мы найдем разность множеств Y и Х, то результат будет выглядеть так: Y \ X = {2; 4}. Таким образом, разность множеств не обладает переместительным (коммутативным) свойством.
Если изобразить множества А и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью.
А \ В
Если множества не имеют общих элементов, то их разность будет изображаться так:
 |
 |
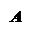А \ В
Если одно из множеств является подмножеством другого, то их разность будет изображаться так:
А \ В
Пересечение – более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в выражении А \ В ∩ С такой: сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А. Что касается объединения и вычитания множеств, то их считают равноправными. Например, в выражении А \ В U С надо сначала выполнить вычитание (из А вычесть В), а затем полученное множество объединить с множеством С.
Вычитание множеств обладает рядом свойств:
1 (А \ В) \ С = (А \ С) \ В.
2 (А U В) \ С = (А \ С) U (В \ С).
3 (А \ В) ∩ С = (А ∩ С) \ (В ∩С).
4 А \ (В U С) = (А \ В) ∩ (А \ С).
5 А \ (В ∩ С) = (А \ В) U (А \ С).
Дата публикования: 2014-11-18; Прочитано: 2826 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
