Объединение множеств

Вновь возьмём множества Х = {0, 1, 3, 5} и Y = {1, 2, 3, 4} и наряду с ними рассмотрим множество {0, 1, 2, 3, 4, 5}. Это множество содержит все элементы множества Х и все элементы множества Y и не содержит никаких других элементов.

Множество, состоящее из всех элементов, принадлежащих или множеству А или множеству В, называется объединением множеств А и В, обозначается А U В. А U В = { х 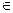А или х 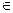В }

Итак, {0, 1, 3, 5} {1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.

Если изобразить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью.

А U В

Если множества не имеют общих элементов, то их объединение выглядит так:

А U В

Если одно из множеств является подмножеством другого, то их объединение будет выглядеть так:

А U В

Часто приходится рассматривать объединение и пересечение трёх и более множеств. Объединение множеств А, В и С есть множество, каждый элемент которого принадлежит хотя бы одному из множеств А, В или С; пересечение множеств А, В и С есть множество всех элементов, принадлежащих и множеству А, и множеству В, и множеству С.

А U В U С 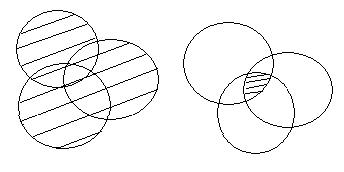А ∩ В ∩ С

Например, объединение множеств остроугольных, тупоугольных и прямоугольных треугольников есть множество всех треугольников.

Еще операции над множествами можно показать с помощью детского анекдота: Однажды лев, царь зверей, собрал зверей на поляне и повелел им разделиться на умных и красивых. После того, как пыль улеглась, лев увидел на поляне две большие группы зверей и мартышку, прыгающую между ними. На вопрос: почему она прыгает туда-сюда, мартышка ответила: «Что мне, разорваться, что ли?». Так вот, мартышка из анекдота – это пример пересечения умных зверей и красивых. А объединением умных и красивых зверей является все множество зверей.

Объединение и пересечение множеств обладают многими свойствами, аналогичными свойствам суммы и произведения чисел:

№ п/п	Свойство операций над множествами	Свойство арифметических операций	Название свойства
		a + b = b + a	Коммутативность
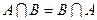
		(а+b)+c = a+(b+c)	Ассоциативность
			Дистрибутивность

Однако эта аналогия не всегда имеет место. Например, для множеств справедливы равенства:

6 (А U С) ∩ (В U С) = (A ∩ B) U С.

7 А U А = А.

8 А ∩ А = А.

Соответствующие равенства для чисел верны не всегда.

Заметим, что, если в выражении есть знаки пересечения и объединения множеств, и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.