Способы задания множеств

Понятие множества мы используем без определения. Но как узнать, является та или иная совокупность множеством или не является?

Считают, что множество определяется своими элементами, т.е. множество задано, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.

Множество можно задать, перечислив все его элементы. Например, если мы скажем, что множество А состоит из чисел 3, 4, 5, и 6, то мы задали это множество, поскольку все его элементы окажутся перечисленными. При этом возможна запись, в которой перечисляемые элементы заключаются в фигурные скобки: А = {3, 4, 5, 6}.

Однако если множество бесконечно, то его элементы перечислить нельзя. Трудно задать таким способом и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множества: указывают характеристическое свойство его элементов.

Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.

Рассмотрим, например, множество А двузначных чисел: свойство, которым обладает каждый элемент данного множества, – «быть двузначным числом». Это характеристическое свойство дает возможность решать вопрос о том, принадлежит какой-либо объект множеству А или не принадлежит. Так, число 45 содержится в множестве А, поскольку оно двузначное, а число 145 множеству А не принадлежит, так как оно не является двузначным.

Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными соседними сторонами и как множество ромбов с прямым углом.

В тех случаях, когда характеристическое свойство элементов множества можно представить в символической форме, возможна соответствующая запись множества. Например, множество А натуральных чисел, меньших 7, можно задать так: А = { х | х 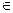N и х < 7}. При такой записи буквой х обозначается элемент множества А. Для этих целей можно использовать и другие буквы латинского алфавита.

Пример 4. Даны множества: М = {2; 3; 5; 7}, N = {-5; -4; -3; -2}, F = {x| x 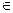Z, -6 < x < -1}, D = {x| x 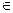N, x < 10, x – простое число}. Какие множества равны между собой?

Решение: Множества F и D заданы характеристическими свойствами. Для того, чтобы сравнить их между собой и с остальными множествами, сформулируем их характеристические свойства словами, а затем зададим их перечислением элементов.

F – множество целых чисел, больших «-6» и меньших «-1». Этому свойству удовлетворяют числа -5, -4, -3, и -2. Из этих чисел состоит множество N. Значит, F = N.

D – множество натуральных чисел, которые меньше 10 и являются простыми. Этому свойству удовлетворяют числа 2, 3, 5 и 7. Из этих чисел состоит множество M. Следовательно, D = M.