Складання характеристичного рівняння. Визначення власних частот кола

За другим законом Кирхгофа t ≥ 0 маємо:

.

Враховуючи те, що , одержуємо диференціальне рівняння другого порядку для вільної складової напруги

.

Характеристичне рівняння при цьому має вигляд:

Характер електромагнітних процесів у контурі залежить від співвідношення параметрів R, L, С, що входять у вираз для коренів характеристичного рівняння

.

Залежно від знака підкореневого виразу корені можуть бути дійсними або комплексно- -спряжені. Вони визначають характер вільних складових перехідних струмів і напруг.

Введемо позначення:

– коефіцієнт загасання вільної складової;

тоді .

В залежності від співвідношення між величинами R, L та С отрима­ємо три варіанти коренів характеристичного рівняння:

а) при 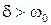корені будуть дійсними та різними, а перехідний процес – аперіодичним;

б) при одержимо два дійсних, однакових кореня , що відповідає граничному аперіодичному режиму. Параметри кола, за яких відбувається цей режим, називаються критичними i між ними існує така залежність: ;

в) при корені p вийдуть комплексно-спряженими

,

а перехідний процес матиме коливальний характер, в якому d характеризує згасання амплітуди коливань, а – їх частоту.