Вирази вільних складових загального розв’язку

Корені характеристичного рівняння	Вирази вільної складової
Корені дійсні й різні
Корені дійсні і рівні
Корені комплексно-спряжені

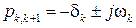
Необхідно пам’ятати, що, оскільки в лінійному колі з часом вільна складова згасає, дійсна складова − коренів характеристичного рівняння, не може бути позитивною.

При дійсних коренях вільна складова перехідної функції 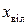монотонно згасає (при ), і має місце аперіодичний перехідний процес. Наявність пари комплексно-спряжених корінь обумовлює появу загасаючих синусоїдальних коливань (коливальний перехідний процес).

Оскільки фізично коливальний процес пов'язаний з періодичним обміном енергій між магнітним полем котушки індуктивності й електричним полем конденсатора, комплексно-спряжені корені можуть мати місце тільки для кіл, що містять обидва типи накопичувачів.

Швидкість загасання коливань прийнято характеризувати відношенням

яке називається декрементом коливання, або натуральним логарифмом цього відношення

,

називаним логарифмічним декрементом коливання, де

Важливою характеристикою при дослідженні перехідних процесів є постійна часу , обумовлена для кіл першого порядку, як:

де – мінімальний по абсолютному значенню корінь характеристичного рівняння.

У випадку коливального процесу (кола другого порядку) перехідна функція у загальному випадку записується рівнянням:

.

Тут і – складові комплексно-спряжених коренів характеристичного рівняння ().

Швидкість загасання вільної складової рівняння залежить від показника δ. Постійну часу у випадку коливального режиму знаходимо як

.

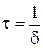Постійну часу можна інтерпретувати як часовий інтервал, протягом якого вільна складова зменшиться у порівнянні зі своїм початковим значенням в е разів. Теоретично перехідний процес триває нескінченно довго. Однак на практиці вважається, що він закінчується при .

Постійні інтегрування A ₁, A ₂ знаходять із початкових умов, які визначають за допомогою законів комутації.

Розрізняють незалежні й залежні (після комутаційні) початкові умови:

– незалежні початкові умови – значення струмів через індуктивності й значення напруг на ємностях, відомі з до комутаційного режиму роботи кола, які по законам комутації не змінюються стрибком

– залежні початкові умови – значення інших струмів і напруг при t = 0 у після комутаційній схемі, обумовлені незалежними початковими значеннями, які знаходяться із законів Кірхгофа для схеми після комутації.