Определение 4.4

Две системы называются равносильными, если каждое решение первой системы является решением второй и наоборот.

Над системами можно производить следующие линейные преобразования:

1) менять уравнения местами;

2) умножать обе части уравнения на любое не равное нулю число;

3) прибавлять к обеим частям одного из уравнений системы соответствующие части другого уравнения, умноженное на любое действительное число.

4.1. Метод Крамера и матричный способ решения системы 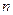линейных уравнений с 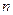неизвестными

Пусть дана система 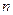линейных уравнений с 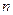неизвестными

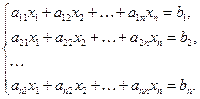(24')

Назовем

(25)

матричным уравнением системы (24')

или , (25')

где .

Покажем, как найти решение системы (25').

Каждую часть равенства (25') умножим слева на обратную матрицу :

(26)

– решение системы (25').

Запишем (26) в развернутом виде:

Таким образом, из определения равенства матриц следует:

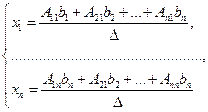или (27)

– формулы Крамера.