 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Логарифмическое дифференцирование
|
|
Производная показательно-степенной функции
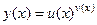
находится с помощью приёма логарифмического дифференцирования. Он состоит в следующем. Сначала надо прологарифмировать (по основанию е) обе части исходного равенства:
 или
или 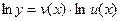 ,
,
затем взять производные обеих частей полученного равенства, применяя формулы для производной сложной функции и для производной произведения:
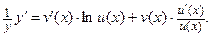
Осталось выразить 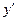 :
:
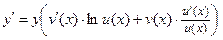
или
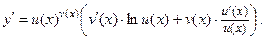
Замечание. При нахождении производной показательно-степенной функции
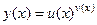
можно пользоваться полученной формулой, но обычно применяется сам приём логарифмического дифференцирования для конкретной функции.
Пример 2.10. Найти производную функции
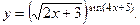
Решение. Прологарифмируем данную функцию:
 .
.
Найдём производные обеих частей полученного равенства:
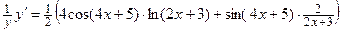
Отсюда находим
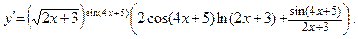
Замечание. Приемом логарифмического дифференцирования удобно пользоваться при нахождении производной функции вида  .
.
Пример 2.11. Найти производную функции
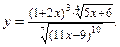
Решение. Прологарифмируем эту функцию:
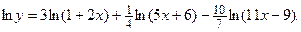
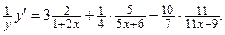

Дата публикования: 2014-11-19; Прочитано: 324 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
