Правила дифференцирования. 1. Производная постоянной равна нулю:

1. Производная постоянной равна нулю:

.

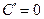2. Производная суммы двух функций равна сумме производных этих функций:

3. Производная произведения двух функций:

В частности,

4. Производная частного двух функций:

5. Производная сложной функции:

если

то

то есть производная сложной функции по независимой переменной х равна произведению производной этой функции по промежуточной переменной u на производную промежуточной переменной по независимой переменной х.

6. Производная обратной функции.

Если 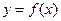– монотонная непрерывная функция, то она имеет обратную функцию ( и ), и их производные связаны равенством

, если .

Пример 2.7. Найти производную функции

Решение. Применим формулы для производной произведения двух функций и производной сло­жной функции:

Пример 2.8. Найти производную функции

Решение. Применим формулу для производной сложной функции:

.

Пример 2.9. Найти производную функции

Решение. Сначала преобразуем исходную функцию, используя свойства логарифма.

.

Найдём производную: