Производная

2.3.1. Определения

Производнойфункции 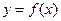называется предел отношения приращения функции к приращению аргумента , когда стремится к нулю:

Рис. 18.

Производная функции 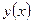по х обозначается 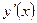или .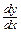

Геометрический смысл производной:

– тангенс угла наклона 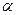касательной к графику функции 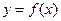в точке с абсциссой 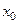(рис. 18).

Физический смысл производной: 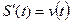– скорость движения тела в момент времени t при прохождении пути .

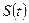Функция, имеющая производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.

Таблица производных

1.			8.
2.		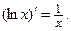	9.
3.			10.
4.			11.
5.		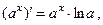	12.
6.			13.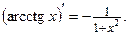
7.