 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Айала Ф., Кайгер Дж. Современная генетика: В 3-х т. Т. 3. Пер. с англ.: – М.: Мир, 1988. – 336 с. Рассчитывая значение хи-квадрат, как и выше, получаем χ2 = 5,26
|
|
Приложение 1. Вероятность и статистика 265
| считаем частоту p аллеля PGM: | ||
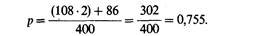
| ||
| Теоретически ожидаемые частоты и численность генотипов составляют | ||
| Генотип | Частота | Численность |
| PGMl/PGMl | р2 = 0,570 | |
| PGMl/PGM2 | 2pq = 0,370 | |
| РGМ2/РGМг | q2 = 0,060 |
Рассчитывая значение хи-квадрат, как и выше, получаем χ2 = 5,26. Каково число степеней свободы в этом случае? Оно равно единице, а не двум, как могло показаться по аналогии с рассмотренным выше случаем менделевского расщепления. Дело в том, что по исходным данным мы рассчитывали, что частота аллеля ρ равна 0,755. Зная это значение и общий объем выборки, мы можем определить ожидаемые численности двух генотипических классов, если знаем число особей в одном из этих трех классов.
Это позволяет сформулировать еще одно правило (аналогичное приведенному выше) для определения числа степеней свободы: число степеней свободы равно разности между числом классов и числом независимых величин, полученных на основе данных, использованных для расчета ожидаемых значений. В рассматриваемом выше случае менделевского расщепления общее число растений было единственным значением, полученным из исходных данных. Зная это значение и законы Менделя, мы можем рассчитать ожидаемое число растений каждого фенотипического класса. В случае проверки равновесия Харди—Вайнберга мы на основе исходных данных рассчитаем два значения: общее число людей в выборке и частоте аллеля р. Заметим, что величина χ2, равная 5,26, статистически достоверна при 5%-ном уровне значимости и одной степени свободы, но статистически не достоверна для двух степеней свободы. Если бы мы ошибочно предположили, что существуют две степени свободы, то не отвергли бы гипотезу о соответствии частот указанных трех генотипов равновесию Харди—Вайнберга.
Предостережение. Метод хи-квадрат - это приблизительный метод, дающий хорошие результаты, только если общий объем выборки и теоретически ожидаемые численности в каждом классе достаточно велики; если же они малы, то данный метод неэффективен. Практически следует руководствоваться двумя правилами: 1) если имеется только одна степень свободы, то ожидаемые значения численности для каждого класса должны быть не меньше пяти; 2) если число степеней свободы больше единицы, то ожидаемые значения численности в каждом классе должны быть не меньше единицы. Существуют, однако, приемы, которыми можно воспользоваться, когда эти условия не выполняются.
Если число степеней свободы равно единице, а численность одного из классов меньше пяти, то следует применять поправку Йетса. Она состоит в том, что, прежде чем вычислить значения хи-квадрат, каждую из разностей между наблюдаемыми и ожидаемыми значениями приближают к нулю на 0,5 единицы. В табл. П.4 приведен расчет значения
Дата публикования: 2014-11-18; Прочитано: 474 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
