Вправи для повторення. 869.Знайдіть значення виразу 4а2 - 4b2, якщо:

868. Спростіть вираз:

а) (2 а - с)² – (2 а + с)² + 8 ас; б) (2 - х ²)(х ² + 2) + (х ² - 2)².

869. Знайдіть значення виразу 4 а ² - 4 b ², якщо:

а) a = 6,75; b = 3,25; б) a = 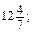b = .

870. Доведіть, що для кожного цілого значення k значення виразу (k + 3)(k ² - k + 4) - (k – 4)(k + 3)² + 32 k ділиться на 48.

871. До 30-відсоткового розчину солі, маса якого дорівнює 750 г, долили 150 г води. Скільки відсотків солі містить утворений розчин?

872. У першому бідоні було молока утричі більше, ніж у другому. Коли з першого бідона перелили 12 л молока у другий, то в другому бідоні його стало в 1,4 разу більше, ніж у першому. Скільки молока було в кожному бідоні спочатку?

873. Швидкість теплохода у стоячій воді дорівнює 28 км/год. Відомо, що за 2 год він проходить за течією річки на 41 км менше, ніж за 4 год проти течії. Яка швидкість течії річки?

Цікаво знати

«В одну ріку не можна увійти двічі» — ці слова приписують давньогрецькому філософу Геракліту Ефеському (з міста Ефес). Вони відображають суттєву особливість реального світу: усе в ньому перебуває у стані безперервної зміни і розвитку. Саме шукаючи закономірності у нескінченному морі видозмін природи, вчені дійшли до понять змінної величини і функції.

Поняття змінної величини вперше було введено в математику французьким математиком Рене Декартом (1596-1650) у його знаменитому творі «Геометрія» у 1637 році. Саме після введення цього поняття починає створюватись сучасне уявлення про функцію як про залежність однієї змінної величини від іншої. Слід зазначити, що хоча деякі залежності між величинами, які ми називаємо функціями, використовувалися ще у давні часи, математика до першої половини XVII ст. залишалася наукою про сталі величини.

Термін «функція» (від латинського functio — виконання, звершення) вперше увів німецький математик Готфрід Віль-гельм Лейбніц у 1694 році. Завдяки працям Лейбніца та відомого англійського фізика й математика Ісаака Ньютона (1643–1727) сформувалася нова гілка математики — математичний аналіз, у якому поняття функції є одним із головних. Лейбніцем та Ньютоном були розроблені методи дослідження функцій, які вже понад 300 років служать потужним засобом вивчення навколишнього світу за допомогою математики.

Готфрід Вільгельм Лейбніц (1646-1716), німецький філософ, математик, фізик

Про вагому роль функцій як математичних моделей реальних процесів Ньютон писав: «Я не зміг би отримати багатьох своїх фундаментальних результатів, якби не відмовився від безпосереднього розгляду самих тіл і не звів усе просто до дослідження функцій».

Запитання і вправи для повторення § 6

1. Наведіть приклад залежності між змінними.

2. Поясніть на прикладі, що таке аргумент і що таке функція.

3. Які ви знаєте способи задання функції? Наведіть приклад функції, заданої за допомогою формули.

4. Що називають областю визначення і областю значень функції?

5. Що називають графіком функції?

6. Як за допомогою графіка функції знайти її значення за відомим значенням аргументу?

7. Яку функцію називають лінійною? Наведіть приклади лінійних функцій.

8. Що є графіком лінійної функції?

9. Яку функцію називають прямою пропорційністю? Наведіть приклади прямої пропорційності.

874. Функція задана формулою у = 5 х – 3.

а) Знайдіть значення функції, які відповідають таким значенням аргументу: –8; 0; 16.

б) Знайдіть значення аргументу, якому відповідає значення функції:
–3; 1.

в) Для якого значення х значення функції дорівнює значенню аргументу?

875. В деяких країнах (наприклад, у США, Канаді) температуру повітря вимірюють у градусах Фаренгейта. Температура в градусах Фаренгейта (t _F) виражається через температуру в градусах Цельсія (t _С) за формулою t _F = 1,8 t _С + 32.

а) Знайдіть t _F, якщо t _С = 20°С; t _С = –15°С.

б) Знайдіть t _С, якщо t _F = 5°F; t _F = 50°F.

в) Знайдіть у градусах Фаренгейта температуру плавлення льоду, температуру кипіння води.

876. Функція задана формулою у = х ² – 3, де змінна х може набувати значень: –3; –2; –1; 0; 1; 2; 3. Задайте цю функцію таблицею.

877. На рисунку 35 зображено графік зміни температури тіла протягом 20 хв.

а) Якою була початкова температура тіла?

б) На скільки градусів збільшилась температура тіла протягом перших 4 хв?

в) На скільки градусів змінилась температура тіла протягом останніх 6 хв?

г) Протягом скількох хвилин температура тіла не змінювалась?

Рис. 35

878. Графіком функції є ламана ABC, де A (-2; 2), B (1; –1), C (5; 1). Накресліть графік функції. Яка область визначення та область значень функції? Чому дорівнюють найбільше та найменше значення функції? Вкажіть нулі функції. Для яких значень х функція набуває додатних значень; від’ємних значень?

879. Побудуйте графік функції у = –3 х – 1. За допомогою графіка знайдіть:

а) значення функції, якщо х = –1,5; х = 1,5;

б) значення х, для якого у = 5.

Побудуйте графік функції:

880. а) y = 2 х + 1, де -3 £ x £ 1; б) y = 0,5 х ² - 0,5, де -2 £ x £ 2.

881. а) у = –3 х; б) у = 1,5 х – 1.

882*. а) у = 2| x |; б) у = х + | x |.

883. Виміри прямокутного паралелепіпеда дорівнюють 1,5 см, 2 см та х см, де х ³ 1. Запишіть формулу, яка задає об’єм паралелепіпеда (у кубічних сантиметрах) як функцію від х. Побудуйте графік цієї функції.

884. Запишіть формулу прямої пропорційності, якщо її графік проходить через точку A (–3; 1).

885. Графік функції y = kx проходить через точку A (–8; 4). Знайдіть k. Чи проходить графік цієї функції через точку: B (2; –1);

886. Знайдіть координати точок перетину графіка функції у = –4 х + 6 з осями координат.

887. Знайдіть координати точок перетину графіків функцій:

а) у = 3 х і у = –3 х + 6; б) у = х + 7 і у = 5 – 4 х.

888*. В одній системі координат побудуйте графіки функцій та . Знайдіть точки перетину графіків. Використовуючи графіки функцій, розв’яжіть рівняння

889*. Функція задана формулою у = kx + 3.

а) Для яких значень k графік цієї функції проходить через точку (2; 4)?

б) Для яких значень k графік цієї функції паралельний графіку функції у = 5 х – 8?

Завдання для самоперевірки № 6

1 рівень

1. Чому дорівнює значення функції у = 2 х – 0,5, якщо х = 1,5?

а) 1,5; б) 1; в) –2,5; г) 2,5.

2. Знайдіть значення функції у = –4 х, якщо х = 0,5.

а) –3,5; б) –4,5; в) –2; г) 2.

3. Для якого значення аргументу значення функції у = 4 х дорівнює 10?

а) 40; б) 2,5; в) 5; г) 2,4.

4. Який із графіків є графіком функції у = 3 х (рис. 36)?

Рис. 36

5. Яка з точок належить графіку функції у = 2 х + 1?

а) A (–4; 9); б) B (4; 9); в) C (4; 7); г) D (–4; –9).

6. Вкажіть правильні твердження:

а) графіком лінійної функції є пряма;

б) формулою у = 5 х – 3 задається пряма пропорційність;

в) графік функції у = 2 х + 3 проходить через точку (5; 2);

г) функція, графік якої зображено на рисунку 36.г), задається формулою у = 3.

2 рівень

1. Функція задана формулою у = 2 х ² – 4. Знайдіть значення функції, якщо х = –2; х = 0,5.

2. Функція задана формулою у = –4 х – 1. Знайдіть значення аргументу, якому відповідає значення функції –9; 9.

3. Користуючись графіком функції (рис. 37), знайдіть: а)значення функції, якщо х = –3; б)значення аргументу, яким відповідає значення функції –2. 4.Побудуйте графік функції у = –2 х. 5.Чи проходить графік функції, заданої формулою у = 4 – х 2 через точку (3; –5)?

Рис. 37

3 рівень

1. Знайдіть область визначення і область значень функції, графік якої зображений на рисунку 37. Для яких значень х функція набуває від’ємних значень?

2. Функція задана формулою у = х ² – 6 х + 2. Знайдіть значення аргументу, яким відповідає значення функції у = 2.

3. Побудуйте графік функції у = –2 х – 2. Вкажіть значення х, яке є нулем функції. Для яких значень х функція набуває від’ємних значень?

4. Знайдіть координати точки перетину графіків функцій у = 3 х – 5 і у = 9 – 2 х.

5. Графік функції у = kх проходить через точку A (2,5; 5). Чи проходить графік цієї функції через точку B (–3; –6)?

4 рівень

1. Знайдітьнайменше значення функції, заданої формулою у = х ² – 6 х + 2.

2. Функція задана формулою у = (х – 2)(х + 4). Знайдіть значення аргументу, яким відповідає значення функції у = –5.

3. Чи проходить графік функції у = 0,4 х + 1,4 через точку перетину графіків функцій у = 3 х + 4 і у = –2 х – 1?

4. За допомогою графіків функцій знайдіть значеннях х, для яких значення функції у = – х + 2 більші, ніж відповідні значення функції у = 0,5 х + 3,5.

5. Побудуйте графік функції, заданої формулою у = 2| x | – 1.

Розділ ІV. СИСТЕМИ ЛІНІЙНИХ РІВНЯЬ ІЗ ДВОМА ЗМІННИМИ
Є чимало задач, розв’язуючи які, отримують рівняння, що містять не одну, а кілька змінних. У даному розділі ми з’ясуємо, що таке лінійне рівняння із двома змінними та його розв’язок, що таке система двох лінійних рівнянь із двома змінними та її розв’язок, які основні способи розв’язу-вання систем лінійних рівнянь із двома змінними.
	— система двох лінійних рівнянь із двома змінними; х = 3, y = 2 — розв’язок цієї системи рівнянь.

§ 7. СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ
ІЗ ДВОМА ЗМІННИМИ

26. Рівняння із двома змінними

1. Поняття рівняння із двома змінними. Ви вже вмієте розв’язувати лінійні рівняння з однією змінною та рівняння, що зводяться до лінійних. Нагадаємо, що лінійне рівняння з однією змінною ¾ це рівняння виду aх = b, де a і b ¾деякі числа, а х ¾ змінна.

Розглянемо приклад, який приводить до рівняння із двома змінними.

Нехай відомо, що сума деяких двох чисел дорівнює 8. Якщо одне із чисел позначити через х, а друге ¾ через y, то матимемо рівняння

х + y = 8,

яке містить дві змінні x та y. Таке рівняння називають рівнянням із двома змінними.

Рівняння

3 х - 2 y = 1, 0 х + 4 y = 5, x ² + y ² = 9, xy = 10

теж є рівняннями із двома змінними. Перші два із цих рівнянь є рівняннями виду aх + by = c, де a, b і с ¾числа. Такі рівняння називають лінійними рівняннями із двома змінними.

Означення

Лінійним рівнянням із двома змінними називають рівняння виду aх + by = c, де x та y ¾ змінні, a, b і с ¾ деякі числа (коефіцієнти рівняння).

2. Розв’язки рівняння із двома змінними. Розглянемо рівняння х + y = 8. Якщо х = 2, y = 6, то це рівняння перетворюється у правильну числову рівність 2 + 6 = 8. Кажуть, що пара значень змінних х = 2, y = 6 є розв’язком рівняння х + y = 8.

Означення

Розв’язком рівняння із двома змінними називають пару значень змінних, для яких рівняння перетворюється у правильну числову рівність.

Розв’язками рівняння х + y = 8 є й такі пари чисел:

х = 4, y = 4; х = 4,5, y = 3,5; х = 10, y = -2.

Скорочено ці розв’язки записують так: (4; 4); (4,5; 3,5); (10; -2). У цих записах на першому місці пишуть значення змінної х, а на другому ¾ значення змінної y. Це пов’язано з тим, щозмінну х умовно вважають першою змінною, а змінну y ¾ другою.

Щоб знайти розв’язок рівняння із двома змінними, можна підставити в рівняння довільне значення однієї змінної і, розв’язавши одержане рівняння з однією змінною, знайти відповідне значення іншої змінної. Для прикладу знайдемо кілька розв’язків рівняння х + y = 8.

Нехай х = 7, тоді 7 + y = 8, звідки y = 8 - 7; y = 1.

Нехай х = -3, тоді -3 + y = 8, звідки y = 8 + 3; y = 11.

Ми знайшли два розв’язки (7; 1) і (-3; 11). Надаючи змінній х інших значень, одержимо інші розв’язки рівняння. Рівняння х + y = 8 має безліч розв’язків.

Шукати розв’язки рівнянь із двома змінними можна іншим способом, який обумовлюється властивостями рівнянь.

3. Властивості рівнянь із двома змінними. Властивості рівнянь із двома змінними такі ж, як і рівнянь з однією змінною, а саме:

1. У будь-якій частині рівняння можна виконати тотожні перетворення виразів (розкрити дужки, звести подібні доданки).

2. Будь-який доданок можна перенести з однієї частини рівняння в іншу, змінивши його знак на протилежний.

3. Обидві частини рівняння можна помножити або поділити на одне й те ж, відмінне від нуля, число.

Розглянемо рівняння

3 х + 2 y = 9.

Використовуючи властивості рівнянь, виразимо з цього рівняння одну змінну через іншу, наприклад, y через х. Для цього перенесемо доданок 3 х у праву частину, змінивши його знак на протилежний:

2 y = -3 х + 9.

Поділимо обидві частини одержаного рівняння на 2:

y = -1,5 x + 4,5.

Користуючись формулою y = -1,5 x + 4,5, можна знайти скільки завгодно розв’язків даного рівняння. Для цього досить узяти довільне значення x і обчислити відповідне значення y. Пари деяких відповідних значень x та y подамо у вигляді таблиці.

x	-4	-3	-2	-1
y = -1,5 x + 4,5	10,5		7,5		4,5		1,5		-1,5

Пари чисел кожного стовпчика ¾ розв’язки рівняння 3 х + 2 y = 9.

Приклади розв’язання вправ

Приклад 1. Знайти значення коефіцієнта а, для яких одним із розв’язків рівняння 3 x + аy = -1 є пара чисел (-1; 2).

● Якщо пара чисел (-1; 2) є розв’язком рівняння 3 x + аy = -1, то має виконуватися рівність 3 × (-1) + а × 2= -1. Розв’яжемо одержане рівняння зі змінною а:

-3 + 2 а = -1; 2 а = -1 + 3; 2 а = 2; а = 1.

Відповідь. а = 1. ●

Усно

890. Серед поданих рівнянь назвіть лінійні рівняння із двома змінними:

a) xy = 3; б) х + 2 y = 7; в) x + y ² = 4;

г) x - y = 1; д) 12 x + 10 y = 0; е) 0 x - 2 y = 3;

є) 3 x + 0 y = 0; ж) 0 x + 0 y = 0; з) 0 x + 0 y = 1.

891. Чи є розв’язком рівняння 2 x - y = 3 пара чисел:

а) х = 2, y = 1; б) х = 1, y = 2?

892. Чи є розв’язками рівняння x + 3 y = 9 пари чисел (1; 1); (6; 1)?

893. Вкажіть кілька розв’язків рівняння x + y = 7.

Рівень А

894. Які з пар чисел (2; 2), (1; 3), (1; 3,5), (4; -1),
є розв’язками рівняння 3 x + 2 y = 10?

895.Які з пар чисел (2; 2), (-1; -2), (1; 1), є розв’язками рівняння
4 x - 3 y = 2?

Знайдіть які-небудь два розв’язки рівняння:

896. а) 2 x + 3 y = 8; б) x - 3 y = -1.

897. а) x + 2 y = 7; б) 3 x - y = 2.

Складіть яке-небудь лінійне рівняння, розв’язком якого є пара чисел:

898. а) х = 1, y = 3; б) (-2, 1).

899. а) х = 2, y = 1; б) (2, -2).

Рівень Б

900. З рівняння 2 x + y = 5 виразіть:
а) змінну х через змінну y;
б) змінну y через змінну x.

Виразіть з рівняння змінну y через змінну x та знайдіть два які-небудь розв’язки рівняння:

901. а) х - y = 7; б) 3 х + 2 y = 15.

902. а) 2 х + y = 5; б) 5 х - 2 y = 10.

903. Серед розв’язків рівняння 3 x + 5 y = 16 знайдіть таку пару чисел, яка складається із двох однакових чисел.

904. Знайдіть значення коефіцієнта а в рівнянні ах + 3 y = 10, коли відомо, що розв’язком цього рівняння є пара чисел (1; 2).

905. Пара чисел (3; 2) є розв’язком рівняння 2 x + by = 12. Знайдіть b.

906. Розв’яжіть рівняння:

а) 0 х - 2 y = 6; б) 3 х + 0 y = 9.

Рівень В

907. Розв’яжіть рівняння в цілих числах (тобто знайдіть усі пари цілих чисел, які є розв’язками рівняння):

а) 2 х - 5 y = 7; б) 3 х + 2 y = 10; в) -4 х + 9 y = 6.

Розв’язання. а) Вибираємо змінну, коефіцієнт біля якої має менший модуль, тобто змінну х. Виразимо цю змінну через змінну y:

2 х - 5 y = 7; 2 х = 5 y + 7; х = y + .

Перетворимо праву частину одержаного рівняння так:

х = y + = 2 y + y + 3 + = 2 y + 3 + (y + 1).

Отже,

х = 2 y + 3 + (y + 1).

Нехай для деяких цілих значень змінних остання рівність є правильною. Оскільки х та 2 y + 3 — цілі числа, то (y + 1) також має бути цілим числом. Отже, y + 1 має ділитися на 2, звідки: y + 1 = 2 k; y = 2 k - 1, де k ¾деяке ціле число. Підставивши y = 2 k - 1 у формулу для змінної х, матимемо:

х = 2(2 k - 1)+ 3 + (2 k - 1+ 1) = 4 k - 2 + 3 + k = 5 k + 1.

Якщо х = 5 k + 1, y = 2 k - 1, то рівняння 2 х - 5 y = 7 перетворюється у правильну числову рівність. Справді,

2(5 k + 1)- 5(2 k - 1) = 10 k + 2 - 10 k + 5 = 7.

Отже, розв’язками рівняння 2 х - 5 y = 7 є пари цілих чисел: х = 5 k + 1; y = 2 k - 1, де k ¾довільне ціле число.

(Надаючи k у формулах для х та y різних цілих значень, одержуватимемо різні цілі розв’язки рівняння 2 х - 5 y = 7. Наприклад, якщо k = 0, то маємо розв’язок х = 1, y = -1; якщо k = 1, ¾ розв’язок х = 6, y = 1.)

908. Знайдіть усі натуральні розв’язки рівняння 5 х + 6 y = 57.

909. Знайдіть усі значення а, для яких одним із розв’язків рівняння 2(5 а + 1)² х - 5(2 а - 1)² у = 7 є пара чисел (2; 5).