 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вправи для повторення. 37. Знайдіть значення виразу:
|
|
37. Знайдіть значення виразу:
а) 2(а + 1) - 4(а - 2), якщо а = -0,1;
б) 1,4 x - (1+ 0,7 x) - (3,3 х - 2), якщо х = 2,25;
в) -2(а + b - 2) - a + 2 b - 4, якщо а = 3; b = -1.
38. У сьомих класах навчається 84 учні, що становить  усіх учнів школи. Скільки всього учнів у школі?
усіх учнів школи. Скільки всього учнів у школі?
39. У місті зараз проживає 52 000 жителів. Відомо, що населення цього
міста щороку збільшується на 4%.
а) Скільки жителів буде в місті через рік?
б) Скільки жителів було в місті рік тому?
3. Лінійні рівняння з однією змінною
Розглянемо рівняння
2 х = –4; –1,7 х = 5,1;  0 х = 2,4.
0 х = 2,4.
Ліва частина кожного із цих рівнянь є добутком деякого числа й змінної, а права частина — деяким числом. Такі рівняння називають лінійними
рівняннями з однією змінною.
| Означення | Рівняння виду aх = b, у якому a і b ¾ деякі відомі числа, а х ¾ змінна, називають лінійним рівнянням з однією змінною. |
Числа a і b називають коефіцієнтами лінійного рівняння.
Коли, розв’язуючи рівняння, виконують певні перетворення, зводячи дане рівняння до більш простого, то в багатьох випадках отим «простим» рівнянням є саме лінійне рівняння.
З’ясуємо, скільки коренів може мати лінійне рівняння. Для цього розглянемо спочатку такі три рівняння:
1) 3 х = 2; 2) 0 х = 2; 3) 0 х = 0.
1) Щоб розв’язати рівняння 3 х = 2, досить обидві його частини поділити на 3. Одержимо один корінь: 
2) У рівнянні 0 х = 2 значення лівої частини дорівнює 0 для будь-якого числа х. Права ж частина рівняння відмінна від нуля. Отже, дане рівняння коренів не має.
3) Рівність 0 х = 0 є правильною для будь-якого числа х. Тому коренем рівняння 0 х = 0 є будь-яке число (рівняння має безліч коренів).
У загальному випадку для лінійного рівняння aх = b матимемо:
якщо а ¹ 0, то рівняння має єдиний корінь 
якщо а = 0, а b ¹ 0, то рівняння коренів не має;
якщо а = 0 і b = 0, то коренем рівняння є будь-яке число (рівняння має безліч коренів).
Підсумок
| aх = b ¾ лінійне рівняння | Коефіцієнти | Корені |
| а ¹ 0 |  ¾ єдиний корінь ¾ єдиний корінь
| |
| а = 0 і b ¹ 0 | коренів немає | |
| а = 0 і b = 0 | коренем є будь-яке число (рівняння має безліч коренів) |
 Для тих, хто хоче знати більше
Для тих, хто хоче знати більше
Рівняння з модулями
Нагадаємо, що модулем додатного числа й числа 0 є це саме
число, модулем від’ємного числа є протилежне йому число:
| а | = а, якщо а ≥ 0; | а | = – а, якщо а < 0.
Так, |1,4| = 1,4; |0| = 0; |–2| = 2. Модуль будь-якого числа x є невід’ємним числом, тобто | x | ³ 0.
Рівняння | x | = 3, | x – 5| = 1, |2 x – 3| = 0, | x | + 3 x = 1 містять змінну під знаком модуля. Такі рівняння називають рівняннями з модулем.
Рівняння виду | x | = a. Розв’язуючи рівняння виду | x | = a, де a — деяке відоме число, можна використовувати геометричний зміст модуля числа: модуль числа
x — це відстань від початку відліку до точки, що зображує число x на координатній прямій.
Розглянемо рівняння | x | = 2. На координатній прямій існують дві точки, розміщені на відстані 2 одиниці від початку відліку. Це точки, що відповідають числам 2
і –2 (рис. 1). Тому рівняння | x | = 2 має два корені: 2 і –2.

Рис. 1
Рівняння | x | = 0 має один корінь — число 0, а рівняння | x | = –2 не має коренів (модуль будь-якого числа x є невід’ємним числом і не може дорівнювати –2).
У загальному випадку рівняння | x | = a:
має два корені a і – a, якщо a > 0;
має один корінь 0, якщо a = 0;
не має коренів, якщо a < 0.
Розв’язування рівнянь з модулями, виходячи з означення модуля числа.
Розв’яжемо рівняння
| x | + 3 x = 4. (1)
Це рівняння не можна звести до вигляду | x | = a, де a — деяке число. Для його розв’язання розглянемо два випадки.
1. Якщо x — невід’ємне число (x ³ 0), то | x | = x і рівняння (1) набуває вигляду x + 3 x = 4, звідки x = 1. Число 1 — невід’ємне (задовольняє нерівність x ³ 0), тому воно є коренем рівняння (1).
2. Якщо x — від’ємне число (x < 0), то | x | = – x і рівняння (1) набуває вигляду
– x + 3 x = 4, звідки x = 2. Число 2 не є від’ємним (не задовольняє нерівність x < 0), тому воно не є коренем рівняння (1).
Отже, рівняння | x | + 3 x = 4 має один корінь x = 1.
 Приклади розв’язання вправ
Приклади розв’язання вправ
Приклад 1.Розв’язати рівняння 5(2 х - 1) = 4 х - 23.
● 10 х - 5 = 4 х - 23; 10 х - 4 х = -23 + 5; 6 х = -18; х = -3.
Відповідь. -3. ●
Приклад 2.Розв’язати рівняння 3 х - 4 = 3(х - 2).
● 3 х - 4 = 3 х - 6; 3 х - 3 х = -6 + 4; 0 х = -2 (або 0 = -2).
Відповідь. Рівняння коренів не має. ●
Приклад 3.Розв’язати рівняння 3 х - 2(х - 1) = х + 2.
● 3 х - 2 х + 2 = х + 2; 3 х - 2 х - х = 2 - 2; 0 х = 0 (або 0 = 0).
Відповідь. Коренем рівняння є будь-яке число. ●
Приклад 4.Розв’язати рівняння 
● Помноживши обидві частини рівняння на 36 (36 ¾ найменше спільне кратне знаменників дробів), матимемо:
 2(2 х - 1) = 3 х + 4; 4 х - 2 = 3 х + 4;
2(2 х - 1) = 3 х + 4; 4 х - 2 = 3 х + 4;
4 х - 3 х = 4 + 2; х = 6.
Відповідь. 6. ●
| Примітка. Розв’язуючи рівняння, варто дотримуватися таких кроків: 1. Якщо у рівнянні є вирази з дробовими коефіцієнтами, то помножити обидві його частини на найменший спільний знаменник дробів. 2. Розкрити дужки. 3. Перенести всі доданки, які містять змінну, в одну частину рівняння (як правило, в ліву), а доданки, які не містять змінної, — в іншу частину (в праву). 4. Звести подібні доданки. 5. Поділити обидві частини рівняння на коефіцієнт біля змінної, якщо він відмінний від нуля. Якщо ж він дорівнює 0, то рівняння або не має коренів, або його коренем є будь-яке число. |
Приклад 5.Розв’язати рівняння 
● 

Якщо модуль числа дорівнює 3, то цим числом є 3 або –3. Тому можливі два випадки:
1) 2 x – 3 = 3; 2 x = 6; x = 3; 2) 2 x – 3 = –3; 2 x = 0; x = 0.
Відповідь. 3; 0. ●
Приклад 6. Розв’язати рівняння 
● 

 z = 4 або z = –4.
z = 4 або z = –4.
Відповідь. –4; 4. ●
Усно
40. Які з даних рівнянь є лінійними рівняннями?
а)  б) 4: х = 2; в) -2,7 y = 0; г)
б) 4: х = 2; в) -2,7 y = 0; г) 
41. Скільки коренів має рівняння:
а) 56 х = 64; б) 0 х = –2; в) 8 х = 0; г) 0 y = 0?
42. Розв’яжіть лінійне рівняння:
а) 6 х = 42; б) 4 х = -12; в) -3 y = 6; г) -5 z = -45;
д) 3 х = -2; е) 0 y = -4; є) 0 х = 0; ж) –2 х = 0.
 Рівень А
Рівень А
Розв’яжіть рівняння:
43. а) 36 х = -54; б) 0,04 z = 1,4; в) 2 y = –  ;
;
г) -1,2 х = -0,09; д) -3,86 t = 7,913; е) 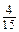 х = -
х = -  ;
;
є)  s =
s =  ; ж) -2,5 х = -
; ж) -2,5 х = -  ; з)
; з)  y = 0,6.
y = 0,6.
44. а) 5 х - 3 = 17; б) 7 х + 32 = 12 х + 25; в) 4 - 3 y = 6 y + 22;
г) 4,5 z + 1 = 7 z + 2,5; д) -1,2 m - 2 = m - 0,9; е) -1,74 х + 7,92 = -1,08 х;
є) 4 y + 1 = -1 + 4 y; ж) 0,77 х = 1,65 + 1,1 х; з) –16,8 х - 3 = 6 х + 2,7.
45. а) 56 х = -196; б) 8 х = –8 + 12 х; в) 1,15 - 3 z = 2,5;
г) 2 y - 18 = -3 y + 67; д) 6 х + 2 = 20 х - 5; е) 4,5 х + 1 = 2 + 4,5 х;
є) 8 - 1,2 z = -6 z + 152; ж) 4,02 t - 1 = 1,52 t; з) 1,7 х + 2,04 = -6,8 х.
46. а) 6(х - 2) = 2 х; б) 3(2 х + 1) = 7 х; в) 1 - (3 х + 1) = 2 х;
г) -2(2 х - 4) = -3; д) 2(х + 5) = 2(х - 4); е) -3(10 - 2 х) = 6 х - 30.
47. а) 8 х - 7 = 3(х – 4); б) –(3 х + 1) = 3(3 – х); в) 6 х – 2 = -2(1 - 3 х).
 Рівень Б
Рівень Б
Розв’яжіть рівняння:
48. а) 2(х - 11) - 5(5 - 2 х) = –23;
б) 8(-3 х + 4) + 14(3 + 2 х) = 4 + 2 х;
в) -5(4 х + 3) + 3 х = -12(х - 3); г) 0,5 х = 0,1(2 х - 5) + 1,7.
49. а) 3,5(х - 3) - 0,7(7 - х) = –7; б) 0,4(2 х - 7) + 1,2(3 х + 0,7) = 1,6 х;
в) 5(4(х + 1) - 9 х) = 25(х + 1); г) 0,8(2,2(х - 1) - 1) - 1,4 х = -0,4.
50. а) 5(3 х - 6) + 4(3 - 2 х) = 5 х - 8; б) 9(х - 3) - 4(7 - 3 х) - 5 = –3 х;
в) -0,3(8 - 4 х) = 0,6(х - 3) + 0,9; г) 2(-0,9 х + 1,4) + 1,4(1,5 + х) = х;
д) 40(5 х - 8(х - 1)) = 160(х + 9); е) 12 + 3(2(х - 1) - 4) = 6(х + 1).
51. Знайдіть значення x, для яких значеннявиразів 2 х - 3 і -3 + 7 х дорівнюють одне одному.
52.Знайдіть значення x, для яких значеннявиразу 25 х - 30 на 5 менше від значення виразу 15 х + 15.
53. Знайдіть значення x, для яких значеннявиразу 4 х + 6 у 6 разів більше від значення виразу 6 х - 15.
Розв’яжіть рівняння:
54. а)  б)
б) 
в)  г)
г) 
55. а) 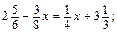 б)
б) 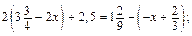
в)  г)
г) 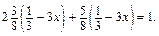
56. а)  б)
б) 
в)  г)
г) 
57. а) | x | = 5; б) | x | = –6; в) | x | = 0;
г) |2 x – 7| = 11; д) |15 – 4 x | = 5; е) |7 x – 2| = 0.
58. а) | x | + 3 = 7; б) 3| x | = 6; в) | x | + 8 = 3.
59. а) |3 x | = 12; б) | x – 3| = 8; в) | x + 2| = –2;
г) | x – 7| = 0; д) 2| x | – 1 = 5; е) 5 – | x | = –11.
 Рівень В
Рівень В
Розв’яжіть рівняння:
60. а) 200(2(2(х - 1) - 1) -1) = -600;
б) 
61. а) |2(х - 3) - (x + 4)| = 2; б) |5 х - 4(2 x + 3)| = 6;
в) 2(| х | - 3) - 4(2| х | + 9) = -48; г) |2 х - 1| - 4(1 - |2 х - 1|) = 6.
62. а) 3 x + | x | = 20; б) 5| x | + x = 12; в) | x | + x = 8;
г) x – | x | = 12; д) x + | x | = 0; е) x – | x | = 0.
63. а) | x | + x 2 = 0; б) x 2 + | x | = –7; в) | x | + |2 x | + 4 = 0.
64. Урівнянні аx = 4389 коефіцієнт а є трицифровим числом виду **1. Розв’яжіть це рівняння, якщо відомо, що його коренем є натуральне
число.
Дата публикования: 2014-11-18; Прочитано: 1676 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
