Химическое равновесие. Обратимые и необратимые реакции. Константа равновесия

Обратимые и необратимые реакции.
Константа равновесия

В ходе самопроизвольного процесса энергия Гиббса уменьшается до определенной величины, принимая минимально возможное для данной системы значение G_min. Дальнейшее изменение энергии Гиббса при неизменных условиях становится невозможным, система переходит в состояние химического равновесия. При его наступлении она не может больше совершать полезную работу, поэтому термодинамическим критерием установления равновесия является следующее уравнение:

∆G = 0

Таким образом, любая химическая реакция протекает самопроизвольно только в направлении, приближающем систему к состоянию равновесия. Причем движущей силой данного процесса является изменение изобарно-изотермического потенциала системы ∆G. Чем ∆G меньше, тем дальше система находится от состояния равновесия и тем более она реакционноспособна. Равновесие может существовать только для обратимых реакций.

По признаку обратимости все химические реакции делятся на обратимые и необратимые.

Необратимые химические реакции при данных условиях самопроизвольно протекают только в одном направлении и при этом получившиеся продукты не взаимодействуют друг с другом с образованием исходных веществ. В связи с этим необратимые реакции заканчиваются либо полным расходованием всех исходных веществ (если они взяты в стехиометрическом соотношении), либо – одного из них, находящегося в недостатке (если исходные вещества взяты в нестехиометрическом соотношении). Реакция с высокой долей вероятности будет необратимой, если при ее протекании выделяется или затрачивается большое количество энергии. Исходя из этого, необратимыми являются реакции горения, многие реакции термического разложения сложных веществ, например:

С + О₂ = СО₂ + Q

СН₄ + 2О₂ = СО₂ + 2Н₂О + Q

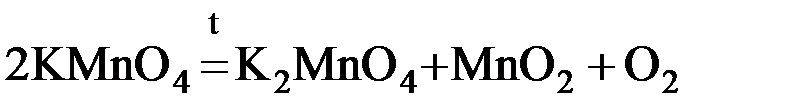
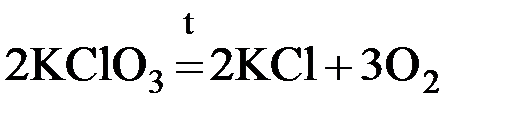
Необратимыми также могут быть реакции, при протекании которых один из продуктов удаляется из сферы реакции в виде осадка либо газа. Это особенно характерно для реакций обмена между электролитами, находящимися в растворенном состоянии, например:

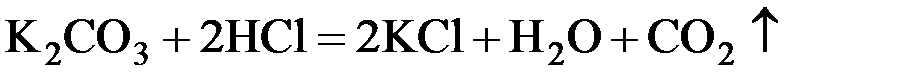
Большинство химических реакций являются обратимыми. Обратимые реакции протекают одновременно в двух противоположных направлениях и не заканчиваются полным расходованием всех, либо одного из исходных веществ, поэтому вместо знака равенства «=» в уравнениях таких реакций ставится знак обратимости «» («↔»).

В начальный момент времени (когда в системе присутствуют только исходные вещества) протекает лишь прямая реакция, идущая слева направо. Скорость ее при этом будет максимальной, но в дальнейшем (по мере расходования исходных веществ и уменьшения их концентрации) скорость прямой реакции будет падать (рис. 13).

В результате протекания прямой реакции в системе появятся и начнут накапливаться конечные вещества, которые будут взаимодействовать между собой. Это приведет к возникновению обратной реакции, идущей справа налево. Скорость ее в начальный момент времени будет равна нулю, но затем (в связи с увеличением концентрации конечных веществ) начнет плавно возрастать (рис. 13).

С течением времени, любая обратимая реакция заканчивается установлением химического равновесия, т.е. такого состояния системы, при котором скорости прямой и обратной реакции становятся равными (рис. 13). Такое равновесие называется динамическим или подвижным, т.к. обе реакции не прекра-

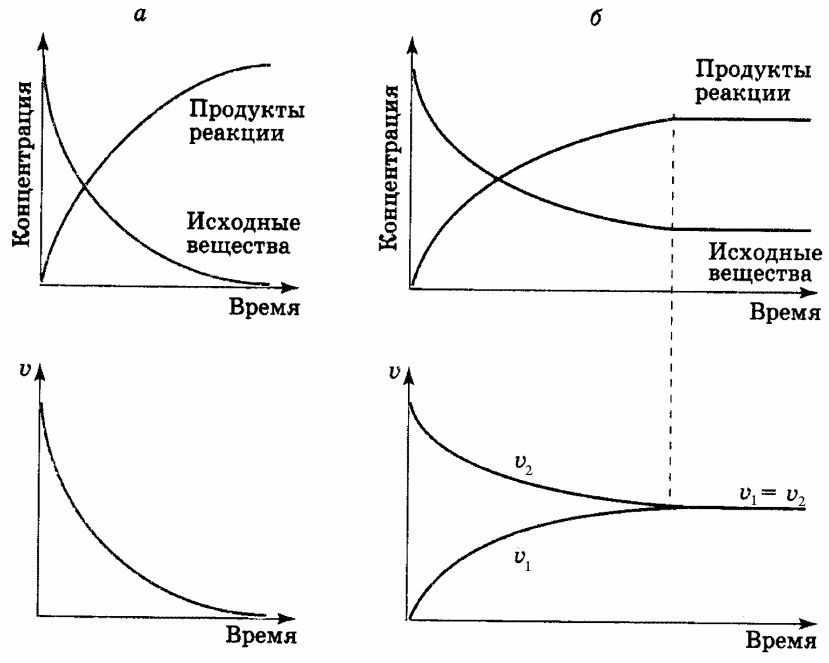
Рис. 13. Изменение концентраций веществ и скоростей необратимой (а) и обратимой (б) реакций.

щаются, но при этом концентрации исходных и конечных веществ остаются неизменными. Они называются иначе равновесными концентрациями.

Это объясняется тем, что в состоянии равновесия число молекул исходных веществ, прореагировавших в единицу времени, равно числу молекул этих же веществ, образовавшихся за то же время из продуктов реакции. До наступления равновесия концентрации исходных веществ непрерывно уменьшаются по сравнению с начальными, а концентрации продуктов реакции, наоборот, возрастают.

Как следует из рисунка 14, состояния химического равновесия в случае обратимой реакции можно достичь двумя путями: из начального состояния системы, в котором находятся только исходные вещества (точка x на графике), либо из начального состояния системы, в котором находятся только продукты реакции (точка y на графике).

Опытным путем было установлено, что для большинства обратимых реакций в условиях их протекания величина |∆G| как прямой, так и обратной реакции обычно не превышает
10 кДж /моль.

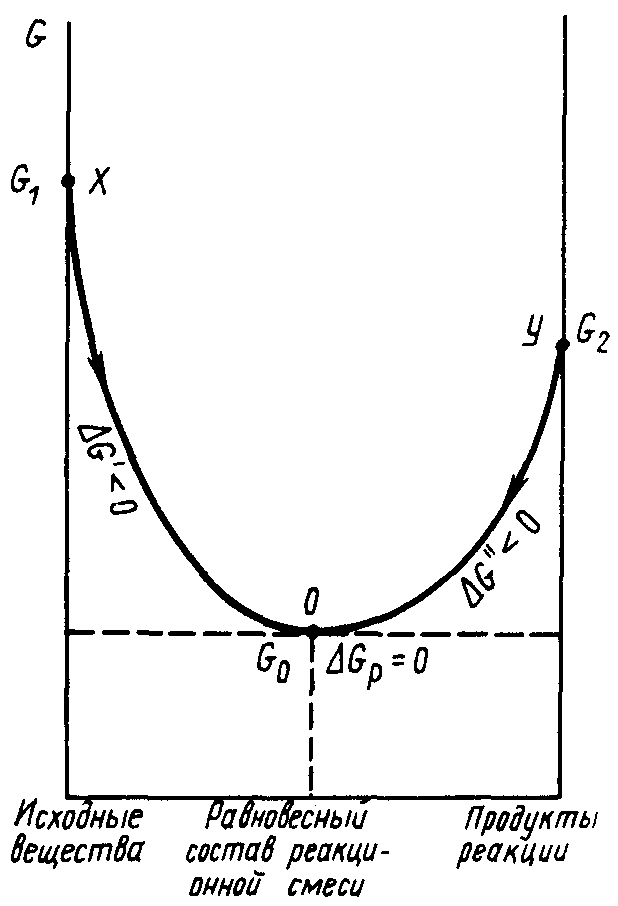
Рис. 14. Изменение энергии Гиббса химической системы при протекании в ней обратимой химической реакции

Если же для одной из реакций |∆G| >> 10 кДж /моль, то она становится необратимой по направлению. Следует иметь в виду, что реакции, необратимые в одних условиях, могут стать обратимыми при их изменении.

Многие реакции являются обратимыми в условиях, отличных от стандартных. В этом случае для расчета ∆G химической реакции в состоянии равновесия необходимо использовать ∆G образования исходных и конечных веществ именно для этих, а не стандартных условий.

Установлено, что если реакция осуществляется в газовой фазе, то ∆G образования 1 моля газа при парциальном давлении p (отличном от стандартного значения) равна

∆G_обр = ∆ + RT ln p

Для реакций, протекающих в растворе, ∆G образования вещества рассчитывается аналогично:

∆G_обр = ∆ + RT ln C

где C – равновесная молярная концентрация растворенного вещества, отличная от стандартного значения, т.е. от 1 моль/л.

Рассмотрим обратимую химическую реакцию, протекающую в газовой фазе

aA + bB ↔ cC + dD

Как известно ∆G химической реакции равно сумме ∆G образования продуктов реакции за вычетом суммы ∆G образования исходных веществ (с учетом их стехиометрических коэффициентов)

∆G_х.р. = с ∆G_обр.С + d ∆G_обр.D – a ∆G_обр.A – b ∆G_обр.B =

= с ∆ 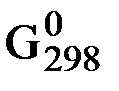С + с RT ln p_С + d ∆ D + d RT ln p_D 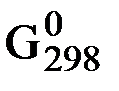– a ∆ A –
– a RT ln p_A – b ∆ 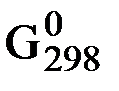B – b RT ln p_B;

Данное уравнение можно преобразовать

∆G_х.р. = с ∆ 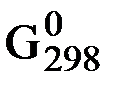С + d ∆ 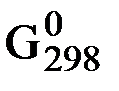D – a ∆ 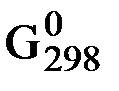A – b ∆ B +

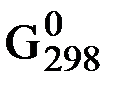∆ х.р.

+ с RT ln p_С + d RT ln p_D – a RT ln p_A – b RT ln p_B;

В окончательном варианте его можно записать таким образом

∆G_х.р. = ∆ 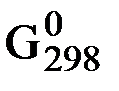х.р. + RT ln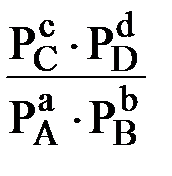

Так как при равновесии ∆G_х.р. = 0, то

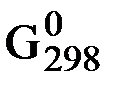∆ х.р. = - RT ln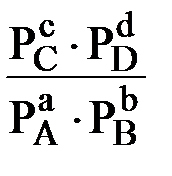

где P_A, P_B, P_C, и P_D являются равновесными парциальными давлениями веществ A, B, C и D.

Как следует из последнего уравнения, выражение под знаком логарифма есть величина постоянная при данной температуре T. Она называется иначе константой химического равновесия K_равн.

Таким образом, для изобарно-изотермических условий

∆G°₂₉₈ х.р. = - RT ln K_равн.

Рассуждая подобным образом, для этой же реакции

aA + bB ↔ cC + dD,

но уже протекающей в растворе, можем вывести аналогичные уравнения:

1) ∆G х.р. = ∆ 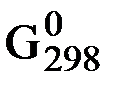х.р. + RT ln