Энтропия. Второй закон термодинамики

Энтропия

На основании первого начала термодинамики невозможно установить, в каком направлении и до какого предела будет протекать тот или иной процесс, связанный с превращением энергии.

Из наблюдений над естественными явлениями в природе известно, что многие из них осуществляются самопроизвольно (т.е. без внешних воздействий) только в определенном направлении.

Так, теплота передается от более нагретого тела к менее нагретому, газ распространяется из области высокого давления в область низкого, вода стекает по склону только вниз, а не наоборот. В обратном направлении указанные процессы идти не могут, т.к. требуют приложения энергии извне. В связи с этим они являются несамопроизвольными.

Характерной особенностью многих самопроизвольных процессов является то, что их протекание сопровождается уменьшением внутренней энергии или энтальпии системы. Это утверждение справедливо и для большинства химических реакций, которые, как правило, являются экзотермическими, если протекают сами по себе.

Наблюдаемые закономерности можно объяснить, если предположить, что любая система из всех разрешенных ей состояний стремится занять то, в котором будет обладать наименьшим (из возможных для нее) значением внутренней энергии или энтальпии. При этом данное состояние для системы будет наиболее устойчивым.

Однако предсказать направленность самопроизвольного протекания физических и химических процессов только за счет стремления системы к достижению минимального значения своей внутренней энергии удается не всегда, т.к. известны многие физические явления и эндотермические химические реакции, которые идут самопроизвольно, но внутренняя энергия системы при этом возрастает.

Примерами таких процессов являются: растворение в Н₂О некоторых твердых солей (NН₄NО₃, NаСl, KNO₃), распад угольной кислоты на газообразный СО₂ и жидкую Н₂О.

Очевидно, существует еще какая-то причина или мотив, влияющие на возможность осуществления тех или иных явлений. Опытным путем установлено, что таким другим поводом для самопроизвольного протекания процессов в природе является стремление системы к максимальному беспорядку, т.е. к достижению неупорядоченного состояния, которое при данных условиях будет для нее наиболее вероятным (рис. 10).

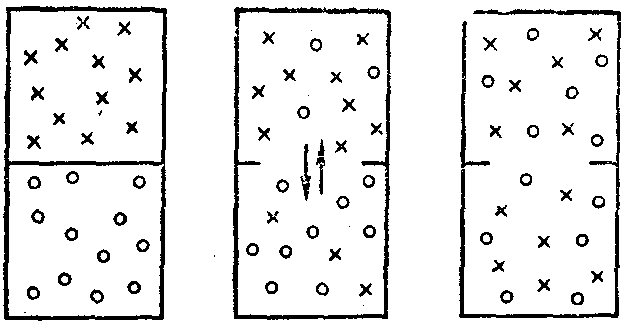
Рис. 10. Схема, иллюстрирующая самопроизвольный процесс выравнивания концентрации

В связи с этим вводится новая термодинамическая функция энтропия (S), являющаяся мерой упорядоченности системы или мерой вероятности достижения ею того или иного состояния.

Термодинамические системы представляют собой совокупность огромного числа структурных единиц вещества: молекул, ионов, атомов, которые участвуют одновременно в различных видах движения: поступательном, вращательном, колебательном и т.д.

Ранее было показано, что любое состояние системы можно описать как с помощью набора ее макроскопических параметров, так и микроскопических. Причем последние учитывают свойства не всей системы в целом, а каждой ее отдельной структурной единицы, т.е. ее расположение в пространстве, скорость и направление движения, характер этого движения, способ и меру взаимодействия с соседними частицами и т.д. Вследствие теплового движения частиц значения их микроскопических параметров будут постоянно изменяться во времени даже в том случае, если макроскопические параметры системы останутся неизменными, вследствие достижения ею равновесного состояния.

Многочисленные наблюдения позволили сделать вывод, что чем большим числом различных микросостояний структурных единиц вещества может быть описано данное макросостояние системы, тем больше вероятность его осуществления и большее значение при этом примет энтропия самой системы.

Принято, что энтропия чистых веществ, существующих в виде идеальных кристаллов при температуре абсолютного нуля (0^оK или –273^оС), равна нулю. Это значит, что в данном случае достигается полная упорядоченность системы, в результате чего всякое движение частиц в узлах кристаллической решетки станет невозможным. Таким образом, данное макросостояние системы может быть реализовано только одним определенным расположением структурных единиц друг относительно друга (иначе говоря, лишь одним их микросостоянием).

При повышении температуры число возможных микросостояний частиц возрастает, т.к. появляются и усиливаются колебательные и вращательные движения атомов, ионов или молекул в узлах кристаллической решетки. В связи с этим число возможных вариантов их расположения друг относительно друга тоже увеличивается.

Энтропия системы возрастает не только с повышением температуры, но и при плавлении либо сублимации твердого вещества, кипении жидкости. Сопровождаются увеличением энтропии и процессы расширения газа, растворения кристаллов, химического взаимодействия, протекающего с увеличением числа молекул либо других структурных единиц вещества.

Все процессы, связанные с увеличением упорядоченности системы: охлаждение, кристаллизация из раствора либо расплава, конденсация газа, сжатие газа, химические реакции, протекающие с уменьшением числа структурных единиц вещества (полимеризация, поликонденсация) – наоборот, сопровождаются уменьшением энтропии.

Так как энтропия системы пропорциональна числу ее равновероятных микросостояний (W), то, согласно уравнению Больцмана, она может быть численно определена следующим образом:

S = k · lgW,

где k – коэффициент пропорциональности, называемый иначе константой Больцмана. Он имеет значение 1,38 · 10^–23 Дж/K и рассчитывается по формуле:

,

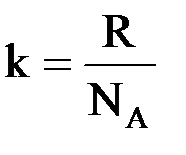где R – универсальная газовая постоянная;

N_A – число Авогадро.

Однако таким образом определить значение энтропии для термодинамической системы нельзя, т.к. не представляется возможным учесть и сосчитать все ее микроскопические состояния.

В 1865 г. Клаузиус предложил другую трактовку понятия энтропии.

Рудольф Клаузиус (1822 – 1888).

Немецкий физик. Ввел понятие энтропии. Обобщив работы Карно, Р. Клаузиус определил функцию S, которая зависит только от начального и конечного состояния обратимого процесса и dS = 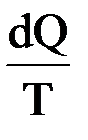. При этом он писал: «Предлагаю величину S назвать энтропией от греческого troph – преобразование. Я специально так подобрал слово энтропия, чтобы оно было созвучно со словом энергия, так как эти две величины настолько сходны по своему физическому значению, что созвучие их кажется мне полезным».

Он исходил из того, что движение частиц в любой системе может быть упорядоченным и неупорядоченным. Между этими двумя видами движения существует принципиальная разница.

Упорядоченное движениеспособно полностью превращаться в неупорядоченное, а переход неупорядоченного движения в упорядоченное никогда не бывает полным. Причина разности между двумя типами движения связана с неодинаковой вероятностью осуществления каждого из них.

Внутренняя энергия идеального газа полностью (а в других системах в значительной степени) определяется неупорядоченным тепловым движением молекул. В то же время совершение работы всегда требует упорядоченного (направленного) движения частиц вещества. Поэтому принципиально невозможно всю внутреннюю энергию системы использовать для совершения работы. Иными словами – любая форма энергии может перейти в теплоту, но теплота преобразуется в другие формы энергии только частично.

Естественность хаотического движения молекул является причиной того, что различные виды энергии стремятся самопроизвольно перейти в теплоту, а теплота передается менее нагретым телам.

Таким образом, запас внутренней энергии системы можно представить в виде двух слагаемых. Ту часть внутренней энергии, которую можно использовать для совершения работы, по предложению Гельмгольца назвали свободной энергией, остальную часть внутренней энергии, которую даже в принципе нельзя превратить в работу, назвали связанной энергией. Она может превращаться только в теплоту и рассеиваться.

Свободная энергия в любой системе заключена в виде потенциальной энергии. По мере совершения системой работы величина ее свободной энергии убывает. Так, более разреженный газ содержит меньше свободной энергии и больше связанной, чем сжатый газ при одной и той же температуре. Следовательно, сжатый газ способен совершить больше полезной работы.

Величина связанной или «обесцененной» части внутренней энергии тем больше, чем меньше разность температур в системе между отдельными ее частями и выше степень неупорядоченности молекул в ней. Таким образом, при самопроизвольных процессах количество свободной энергии в системе должно уменьшаться, а связанной, наоборот, увеличиваться.

Мерой изменения связанной энергии при переходе системы из одного состояния в другое Клаузиус предложил считать изменение ее энтропии. Он показал, что для изотермических обратимых процессов изменение энтропии равняется тепловому эффекту процесса, деленному на температуру системы (в градусах Кельвина):

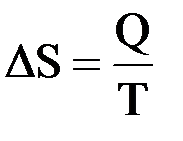
Для изобарных процессов, в ходе которых температура системы изменяется от Т₁ до Т₂ и ее агрегатное состоянии остается одним и тем же, ΔS определяется более сложным образом:

При этом, если Т₁ = 0; то ΔS = S_Т – S₀,

где S₀ – энтропия системы при абсолютном нуле; S_Т – энтропия системы при температуре Т.

Если S₀ = 0, то ΔS = S_Т, а значит

Верхнее выражение позволяет рассчитать энтропию при любой температуре, если известна зависимость изобарной теплоемкости системы (С_р) от температуры в интересующем нас интервале. При температуре плавления и температуре кипения энтропия вещества увеличивается скачкообразно (рис. 11) и ее прирост ΔS можно рассчитать по формуле

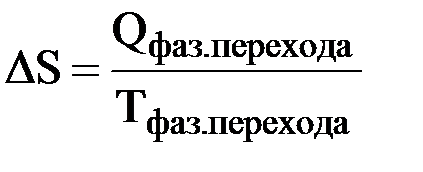
где Q_{фаз. перехода} – теплота, затраченная на плавление или кипение вещества; Т_{фаз. перехода} – температура плавления или кипения вещества.

В общем случае энтропию любого вещества при некоторой температуре Т можно рассчитать по формуле

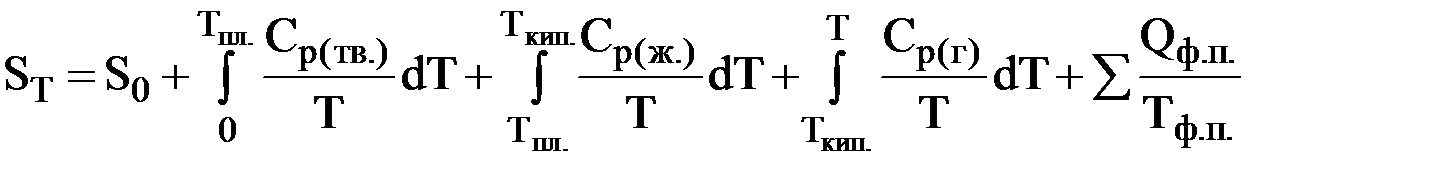
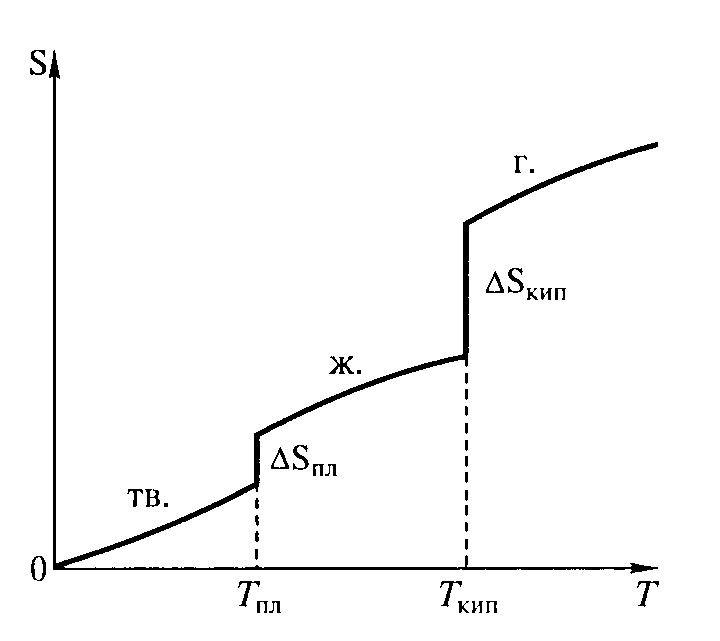
Рис. 11. Зависимость энтропии некоторого вещества от температуры (тв. – твердое вещество; ж. – жидкость; г. – газообразное вещество)

Энтропию вещества, найденную таким образом (т.е. относительно S₀ = 0), называют абсолютной энтропией .

Значения энтропии различных чистых веществ, определенные в расчете на один их моль или для растворов веществ с молярной концентрацией 1 моль/дм³ при Т = 298K и р = 101,325 кПа называются стандартными энтропиями и являются справочными величинами (табл. 3).

Единица измерения энтропии для вещества (так называемая «энтропийная единица» или сокращенно – э.е.) имеет размерность Дж/моль · K.

Изменение энтропии при протекании какой-либо химической реакции можно вычислить таким же способом, как и изменение энтальпии, т.е. из суммы энтропий продуктов реакции следует вычесть сумму энтропий исходных веществ (с учетом стехиометрических коэффициентов):

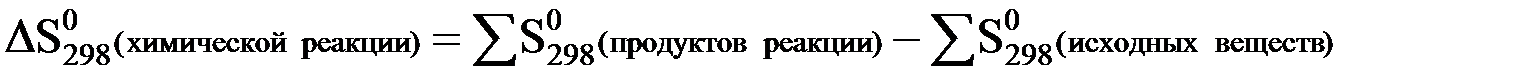
Например, для химической реакции:

4NH_{3 (г)} + 3O_{2 (г)} = 2N_{2 (г)} + 6H₂O_(ж)

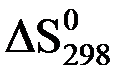= ( (N_2(г)) + (H₂O_(ж)) – (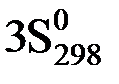 (O_2(г)) + 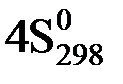(NH_3(г))

Таблица 3. Стандартные энтропии некоторых веществ
(Дж/моль • К)

Вещество	S°298	Вещество	S°298	Вещест-во	S°298	Вещество	S°298
Al (г.) Al (тв.) Al3+ (р.) AlCl3(тв.) AlBr3(тв.) Al2O3(тв.) Fe (г.) Fe (тв.) Fe3+(р.) FeO (тв.) Fe2O3 (тв.) NaCl (тв.)	164,4 28,35 -301 109,3 180,2 50,92 180,4 27,15 -309,3 60,75 87,4 72,12	Cl2 (г.) Cl (г.) Cl-(р.) HCl(г.) HCl(р.) ClO2(г.) Cl2O(г.) Br2 (г.) Br2 (ж.) HBr (г.) HI (г.) CaO(тв.)	229,9 165,1 56,54 186,8 56,5 257,0 266,2 245,5 152,2 198,6 206,5 39,7	N2 (г.) NH3 (г.) NH4+(р.) NH4Cl(тв.) NO (г.) NO2 (г.) N2O4 (г.) HNO3 (г.) NO3-(р.) Pбел (тв.) Pкрас (тв.) CO2 (г.)	199,9 192,6 114,4 95,8 210,6 240,1 304,3 266,9 147,3 41,1 22,8 213,68	H2O (г.) H2O(ж.) H2O(тв.) H2 (г.) H+(р.) OH-(р.) O2 (г.) O3 (г.) SO2(г.) SO3 (г.) H2S(г.) CaCO3(тв.)	188,72 70,08 39,33 130,6 -10,87 205,04 238,8 248,1 256,4 205,7 92,9

Энтропия является функцией состояния (ее изменение не зависит от пути процесса) и экстенсивным свойством системы (т.е. общая энтропия системы равна сумме энтропий ее составных частей).

В изолированных системах самопроизвольно могут протекать только те процессы, которые сопровождаются увеличением энтропии. Это означает, что состояние устойчивого термодинамического равновесия в такой системе возникает в том случае, если величина ее энтропии достигает своего максимально возможного значения.

Для неизолированных, т.е. закрытых и открытых систем только изменение энтропии, как и изменение одной внутренней энергии, уже не является критерием возможности самопроизвольного протекания процесса.

Второе начало термодинамики.
Свободная энергия Гиббса

Первое начало термодинамики дает строгое количественное описание того, как изменяется энергия любой системы в результате обмена ею с окружающей средой в форме теплоты, работы или передачи вещества. Но оно не позволяет определить условия, при которых термодинамические процессы будут протекать самопроизвольно, вплоть до наступления равновесия, а также спрогнозировать их направленность. Для выяснения этих вопросов, имеющих большой теоретический и практический интерес, используется второе начало (второй закон) термодинамики.

В термодинамических системах, как было показано ранее, наряду с уменьшением энтальпии, направленность любого физического и химического процесса определяется еще и изменением энтропии. Причем действие этих факторов часто приводит к взаимнопротивоположным результатам.

Так, при протекании химических реакций энтальпийному фактору (ΔН < 0), действующему в направлении агрегации атомов, ионов либо молекул в более сложные частицы за счет реализации сил химической связи и межмолекулярного воздействия, и способствующему упорядочиванию системы, противостоит энтропийный фактор (DS > 0), инициирующий процессы дезагрегации молекул, т.е. распад их на более простые и меньшего размера частицы, и увеличению вследствие этого энтропии.

Для сопоставления и сравнения действия данных факторов их необходимо выразить в одинаковых единицах измерения. Так как изменение энтальпии (ΔН) измеряется в Дж/моль, а изменение энтропии (DS) – в Дж/моль · K, необходимо умножить DS на Т. В результате этого размерность произведения Т · DS станет такой же, как и у изменения энтальпии, а именно:

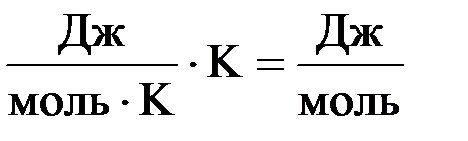
Умножение DS на Т вполне правомерно, т.к. повышение температуры усиливает различные виды движения частиц, а значит и их беспорядок, приводя тем самым к возрастанию энтропии.

При отсутствии энтропийного фактора (DS = 0) самопроизвольно могут идти процессы, сопровождающиеся положительным тепловым эффектом (ΔН < 0).

Если система изолирована, обмена энергии с внешней средой нет (ΔН = 0), а значит отсутствует энтальпийный фактор, то самопроизвольно будут идти процессы, сопровождающиеся увеличением энтропии (DS > 0).

В том случае, когда в системе действуют оба фактора, направление процесса определяется их суммарным влиянием, причем уменьшение энтальпии характеризует стремление системы к порядку, увеличение энтропии – к беспорядку.

Если система находится в состоянии равновесия, то, очевидно, справедливо равенство:

ΔН = ТDS или ΔН – ТDS = 0.

Опытным путем установлено, что для самопроизвольно идущих процессов при условии одновременного действия энтропийного (DS > 0) и энтальпийного (ΔН < 0) факторов справедливо соотношение:

ΔН – ТDS < 0 или (Н₂ – Н₁) – Т(S₂ – S₁) < 0.

Преобразовав это неравенство, получим:

(Н₂ – ТS₂) – (Н₁ - ТS₁) < 0.

Функцию (Н – ТS) называют изобарно-изотермическим потенциалом (сокращенно – изобарным потенциалом) или свободной энергией Гиббса и обозначают буквой G. Она названа таким образом в честь американского физика, автора классических трудов по химической термодинамике Гиббса Джозайя Уилларда.

Этот новый термодинамический параметр относится к функциям состояния, так как его изменение определяется только начальным и конечным состоянием системы, но не зависит от пути и способа ее перехода из одного состояния в другое.

Понятие химического потенциала ввел в своей работе «О равновесии гетерогенных веществ» американский физик-теоретик, один из основоположников термодинамики и статистической механики
Дж. Уиллард Гиббс (1839 – 1903). В этой статье он разработал теорию термодинамических потенциалов, доказал правило фаз (общее условие равновесия гетерогенных систем), создал термодинамику поверхностных явлений и электрохимических процессов; обобщил принцип энтропии, применив второе начало термодинамики к широкому кругу процессов, и вывел фундаментальные уравнения, позволяющие определять направление реакций и условия равновесия для смесей любой сложности. Многие идеи современной равновесной термодинамики берут начало из этих работ Дж. Гиббса.

В условиях постоянного давления и температуры (p = const и T = const) любой физический или химический процесс самопроизвольно может протекать только в том случае, если он сопровождается уменьшением изобарно-изотермическо-го потенциала системы (G₂ – G₁ = DG < 0). Это определение составляет сущность второго закона или второго начала термодинамики.

Для процессов, идущих при постоянной температуре и объеме, вводится соответствующая функция F = U – TS, которая называется иначе изохорно-изотермическим потенциалом или свободной энергией Гельмгольца. В системах, находящихся при данных условиях (V = const и T = const), самопроизвольно могут осуществляться процессы, сопровождающиеся уменьшением изохорно-изотермического потенциала (DF < 0).

Соотношение между термодинамическими функциями U, H, G и F представлено на рис. 12.

Энергия Гиббса (как и энергия Гельмгольца) характеризует способность системы совершать полезную работу, т.е. определяет ту часть ее внутренней энергии (называемой иначе свободной энергией), которая в изобарно-изотермических (или изохорно-изотермических условиях), может превращаться в работу (отличную от работы расширения системы).

Рис. 12. Соотношение между термодинамическими функциями
U, H, G и F

Величина DG или DF при термодинамически обратимом процессе равна максимально полезной работе, которую может совершить система, или меньше ее при необратимом процессе, т.к. часть свободной энергии при этом рассеивается в виде теплоты и превращается в связанную энергию.

В связи с этим можно дать другое определение второго начала термодинамики. В неизолированных системах самопроизвольно могут протекать лишь те процессы, в ходе которых совершается полезная работа против внешних сил.

Для химических реакций, протекающих в человеческом организме, а также в лабораторных или производственных условиях (при p = const и T = const) принципиальное значение имеет изменение свободной энергии Гиббса (DG).

Если величина DG имеет отрицательный знак (DG < 0), то реакция самопроизвольно может протекать только в прямом направлении. Причем абсолютное значение разности DH – TDS = DG будет определять движущую силу данного процесса.

Если же DG > 0, то в условиях, для которых были измерены DH и TDS, в прямом направлении данная реакция протекать не может. Зато осуществимой окажется обратная реакция, для которой DG будет иметь отрицательное значение.

Необходимо отметить, что отрицательные значения DG (или DF) определяют только принципиальную возможность самопроизвольного осуществления процесса, но ничего не говорят о скорости и условиях, необходимых для его начала.

Так, для химической реакции горения различных органических и неорганических веществ уже при комнатной температуре DG << 0, но эти вещества начинают гореть только при нагревании. Во многих случаях, чтобы увеличить скорость реакции, при определенных условиях необходимо использовать катализаторы, подбирать соответствующие концентрации исходных веществ.

Величина и знак DG для многих реакций зависит от температуры процесса. В этом случае, в зависимости от условий, принципиальная возможность протекания реакции в том или ином направлении может изменяться.

Реакции, для которых DH < 0, а DS > 0, могут самопроизвольно протекать в прямом направлении при любых температурах, т.к. DG у них всегда будет меньше нуля. Примером такой реакции может служить гидролиз пептидов или белков.

Если для химической реакции DH > 0, а DS < 0, то ее самопроизвольное протекание в прямом направлении всегда неосуществимо, т.к. энергия Гиббса в данном случае возрастает. Примером такой реакции может служить процесс фотосинтеза – образование глюкозы и кислорода из углекислого газа и воды, – который невозможен без участия солнечной энергии.

В случае DH > 0 и DS > 0 самопроизвольному протеканию реакции в прямом направлении способствует энтропийный фактор. При низких температурах отрицательное значение DH – TDS может быть невозможно, но при нагревании – оно возможно и реакция становится осуществимой в прямом направлении. Например, тепловая денатурация белковых молекул.

Если DH < 0 и DS < 0, то отрицательное значение DG такой химической реакции наблюдается только при достаточно низких температурах.

При вычислении DG в химической реакции можно использовать следствие из закона Гесса, применяемое для расчета ее теплового эффекта (изменения энтальпии). В данном случае оно будет звучать следующим образом.

Изменение энергии Гиббса химической реакции равно алгебраической сумме DG образования продуктов реакции за вычетом алгебраической суммы DG образования исходных веществ (с учетом их стехиометрических коэффициентов).

DG _{химич. реакции} = SDG _{обр. конечных веществ} – SDG _{обр. исходных веществ}

где DG _обр. – изменение энергии Гиббса химической реакции, в ходе которой образуется 1 моль сложного вещества из соответствующих простых веществ.

Значение DG обр. для вещества зависит от температуры и давления реакции, поэтому его, как правило, определяют для стандартных условий (Т = 298 K и р = 101,325 кПа, концентрация вещества в растворе = 1 моль / дм³) и обозначают . Значения определены для многих соединений и приводятся в соответствующих справочниках или таблицах. Величину для простых веществ, устойчивых при стандартных условиях, принять равной 0.

Для химических реакций:

Fe₂O_3(к) + 3CO_(г) = 2Fe_(к) + 3CO_2(г)

изменение энергии Гиббса можно рассчитать следующим образом (с учетом таблицы 4)

D = (3D 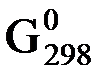_обр.(СО_2(г)) – (3D _обр.(СО_(г)) + D _обр.(Fe₂O_3(к)) = 3 · (–393,5) – 3 · (–110,5) + (–822,2) = –1180,5 – (1153,7) =
–26,8 (кДж).

Если D 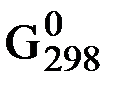<< 0, то можно считать, что осуществимо самопроизвольное протекание реакции в прямом направлении не только при стандартных условиях, но и в широком диапазоне более высоких температур. Неравенство D 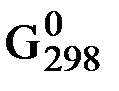>> 0 отвечает принципиальной невозможности протекания процесса в прямом направлении как при Т = 298^оK, так и в других условиях. К сожалению, не существует определенных минимальных значений D , за пределами которых процесс можно считать в принципе реализуемым в прямом (DG < 0) или в обратном (DG > 0) направлениях.

Таблица 4. Стандартные величины А/С 298 некоторых веществ (кДж/моль)

Вещество	∆ G °298	Вещество	∆ G °298	Вещест-во	∆ G °298	Вещество	∆ G °298
AgCl (тв.) Ag2O(тв.) Al3+ (р.) AlCl3 (тв.) AlBr3 (тв.) Al2O3 (тв.) CO (г.) CaCO3(тв.) CO2 (г.) FeBr3 (тв.) Fe2O3 (тв.)	-109,8 -31,1 -490,5 -628,6 -490,6 -1582 -110,5 -1128,8 -393,5 -246 -822,2	NaCl(тв.) NaF(тв.) LiF (тв.) Cl- (р.) HCl (г.) HCl (р.) ClO2(г.) Cl2O(г.) HF (г.) HBr(г.) HI (г.)	-384,1 -543,3 -584,1 -131,4 -94,79 -131,2 122,3 -272,8 -51,2 1,78	NH3 (г.) N2H4 (г.) NH4Cl(тв.) NO (г.) NO2 (г.) N2O4 (г.) HNO3(г.) Pбел (тв.) Pкрас (тв.) P4O10 (тв.) PH3 (г.)	-16,71 159,28 -203,2 86,58 51,5 98,29 -74,8 -11,9 -2697,8 13,39	H2O(г.) H2O(ж.) H+(р.) OH-(р.) O3 (г.) H2O2(ж.) H2S(г.) H2Se(г.) H2Te(г.) SO2 (г.) SO3 (г.)	-228,61 -237,24 -157,42 162,7 -120,4 -33,8 -19,7 - -300,2 -370