Законы движения толкателя внутри фазовых углов

Изменение кинематических параметров толкателя в ходе выполнения технологического процесса лимитируется законом движения. Под законом движения понимается, как правило, изменение аналогов ускорений толкателя по углу поворота кулачка. Ниже приведены чаще всего употребляемые законы изменения аналогов ускорений: синусоидальный, косинусоидальный, с постоянным и линейно изменяющимся ускорением.

Синусоидальный закон движения толкателя. Аналоги ускорения на фазе удаления изменяются по зависимости

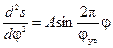, (6.1)

где А – амплитуда гармонической функции; 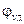– значение фазового угла удаления; – текущее значение угла поворота кулачка.

Интегрируя выражение (6.1), получим для аналогов скоростей толкателя следующую зависимость:

, (6.2)

где С ₁– постоянная интегрирования.

И, наконец, интегрируя выражение (6.2), получим формулу для перемещения конца толкателя:

, (6.3)

где С ₂ – постоянная повторного интегрирования.

Поскольку постоянные интегрирования С ₁ и С ₂ полностью определяются начальными условиями задачи, то, принимая в момент начала движения конца толкателя s = 0, , получим

. (6.4)

Для определения амплитуды А используется граничное условие .

Следовательно, из закона движения (6.3) с учетом постоянных (6.4) имеем

. (6.5)

Таким образом, с учетом формул (6.3) – (6.5) закон перемещения толкателя на фазе удаления принимает следующий вид:

. (6.6)

Дифференцируя (6.6), для аналога скорости толкателя получим

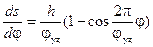. (6.7)

На основании формул (6.6), (6.7) можно определить численные значения перемещений s_i (j _i), аналогов скорости (j _i) и построить график синусоидального закона движения для любых числовых значений φ_i(i = 0,1,2…n), если 0 £ j _i £ j_уд. Как правило, углы j _i отстоят друг от друга с постоянным шагом, например, 10°.

На фазе дальнего стояния координата конца толкателя постоянна
s (φ) = h и не зависит от угла поворота кулачка. Вместе с тем угол поворота кулачка увеличивается и в конце фазы дальнего выстоя толкателя будет равен φ_c = φ_уд + φ_д.с

Если синусоидальный закон используется для фазового угла приближения, то математическая зависимость аналогов ускорений от угла поворота кулачка принимает следующий вид:

, (6.8)

где – амплитуда гармонической функции на фазе приближения толкателя к центру вращения кулачка; φ– текущее значение угла поворота кулачка, причем область определения .

Интегрируя дважды выражение для аналогов ускорений (6.8), найдем, что перемещение конца толкателя осуществляется по закону

. (6.9)

Непосредственной подстановкой значения в закон движения (6.9) можно убедиться, что , т.е. толкатель вышел на окружность минимального радиуса кулачка.

Косинусоидальный закон движения толкателя. Аналоги ускорений при 0 ≤ φ ≤ φ_уд. для фазы удаления толкателя от центра вращения кулачка в этом случае определяются функцией

(6.10)

и функцией

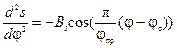(6.11)

для фазы приближения толкателя. В формулах (6.10) и (6.11) принято: A ₁, B ₁– амплитуды гармонической функции для каждой из фаз; φ_c– суммарный угол поворота кулачка перед началом фазы приближения согласно (6.11) меняется в пределах .

Дважды интегрируя (6.10), получим закон перемещения толкателя на фазе удаления:

. (6.12)

Аналогично на основании (6.11) получим формулу

, (6.13)

которая определяет закон движения толкателя на фазе приближения.

Закон линейно-убывающих аналогов ускорений. На фазе удаления толкателя при имеем

, (6.14)

где А ₂– начальное значение аналога ускорений.

При начальных условиях φ = 0, s = 0, после двукратного интегрирования (6.14) получим перемещение

(6.15)

Используя граничное условие φ = φ_уд, s = h имеем для начального значения аналогов ускорений

. (6.16)

На основании (6.15) с учетом (6.16) имеем для фазы удаления следующий закон перемещений толкателя:

(6.17)

Аналогично для получают закон перемещений толкателя для фазы приближения:

(6.18)

Формулы (6.17), (6.18) полностью определяют закон перемещения толкателя при линейном законе изменения аналогов ускорений.

Закон постоянных аналогов ускорений внутрифаз (параболический по перемещению толкателя). Для этого закона характерно мгновенное изменение знака аналога ускорений внутри фазового угла (см. рис. 6.1). Известно [4], что разрыв функции ускорений является признаком так называемого мягкого удара. Представление об ударе не является буквальным, а связано с изменением знака сил инерции действующих на толкатель. В этом смысле мгновенный отрыв толкателя от поверхности кулачка, равно как и мгновенное прижатие, являются ударами.

Допустим, что на фазе удаления толкателя при положительное значение аналога ускорений

(6.19)

Интегрируя (6.19) при начальных условиях φ = 0, , получим

(6.20)

Как видно из рис. 6.1, высота треугольника аналога скорости равна площади прямоугольников аналогов ускорений. Поэтому имеет место соотношение

, (6.21)

где k – коэффициент, зависящий от участков с положительными и отрицательными ускорениями на фазовом угле удаления. Обычно

0 < k <1.

Поскольку φ₁ + φ₂ = φ_уд, то

,

. (6.22)

Рис.6.1. Закон движения толкателя с постоянными значениями

аналогов ускорений внутри фазовых углов

Интегрируя (6.20) при с положительным ускорением, получим на участке φ₁ закон перемещения толкателя:

. (6.23)

Чтобы найти аналитические зависимости на участке, где аналог ускорения отрицательный, необходимо последовательно интегрировать

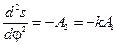, (6.24)

используя при этом начальные условия согласно формулам (6.20) и (6.23). Итак, при φ₁ £ j£ j_уд имеем

, (6.25)

. (6.26)

Используя граничное условие , а также формулы (6.22), находим

. (6.27)

Таким образом, при асимметрии изменения аналогов ускорений на фазе удаления на каждом участке для описания необходимо свое аналитическое выражение.

Пусть для фазы приближения задан симметричный закон движения, как на рис. 6.1. Для аналогов ускорений имеем

. (6.28)

Будем считать, что угол поворота меняется в пределах 0 £ j£ j_пр . При отрицательном значении аналога ускорений (–В) после интегрирования (6.28) получим

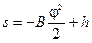, (6.29)

а при положительном В и имеем

. (6.30)

Из граничного условия s(φ_пр) = 0 находим . Следует иметь ввиду, что если в формуле (6.27) принять k = 1, то получим тот же результат для фазы удаления.

Закон линейно-возрастающих аналогов ускорения. При этом законе происходит мгновенное изменение ускорений внутри фазовых углов, то есть имеет место мягкий удар.

На фазе удаления толкателя при симметричном исполнении закона для угла поворота кулачка на интервале аналоги ускорений изменяются по такой зависимости:

. (6.31)

Последовательно интегрируя выражение (6.31) при начальных условиях j= 0, s = 0, , получим для аналога скорости и перемещения следующие выражения:

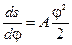, (6.32)

. (6.33)

Обычно ход толкателя известен заранее по условию задачи. Допустим, что при φ = φ_уд имеем s = h. Тогда

и, следовательно,

. (6.34)

Таким образом, постоянная А зависит от проектных параметров. Для дальнейшего описания закона движения толкателя на фазе удаления при , аналоги ускорений по условию симметрии будут иметь вид

. (6.35)

При интегрировании функции (6.35) начальными условиями для определения постоянных интегрирования согласно (6.32), (6.33) будут следующие значения:

, .

Графическое представление закона линейно-возрастающих аналогов ускорений показано на рис. 6.2.

В результате интегрирования аналога ускорений (6.35) при известных начальных условиях получим для аналогов скорости следующее выражение:

, (6.36)

а для перемещений

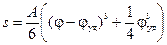. (6.37)

Таким образом, на фазе удаления закон перемещения толкателя по углу поворота кулачка описывается последовательно с помощью зависимостей (6.33), (6.37). При этом постоянная А вычисляется по формуле (6.34).

Математическое описание закона линейно-возрастающих аналогов ускорений на фазе приближения проще всего провести с помощью линейной замены аргумента ψ = φ – φ_д.с – φ_уд. Это равносильно тому, что угол поворота кулачка jна фазе приближения заменяется изменением параметра 0 £ y£ j_пр. Обозначим коэффициент линейной функции аналогов ускорений на фазе приближения через В.

При 0 £ y£ имеем .

Аналоги скорости

, (6.38)

а перемещения

. (6.39)

Рис. 6.2. Закон движения толкателя с линейно-возрастающими аналогами ускорений внутри фазовых углов

Постоянные интегрирования определяется из условий: y= 0,

,

C ₁ = 0, s (0) = h, C ₂= h. Следовательно, постоянная

.

Если параметр лежит в пределах , то для определения перемещений толкателя по углу поворота получим следующую функцию:

, (6.40)

а для аналогов скорости

. (6.41)

Наличие мягких ударов внутри фазовых углов движения не является обязательным признаком. К законам движения толкателя с мягкими ударами относят также описанные ранее косинусоидальный и линейно-убывающие аналоги ускорений. У этих законов разрыв функции ускорений происходит при переходе толкателя с одной фазы на другую.

Линейный закон перемещения толкателя. Этот закон обеспечивает постоянство аналогов скорости толкателя внутри фаз движения.

На фазе удаления перемещение толкателя пропорционально углу поворота кулачка:

. (6.42)

На фазе приближения также имеет место линейная функция

. (6.43)

Дифференцируя (6.42) или (6.43), получим постоянное значение аналога скорости. Если до перехода, например, на фазу удаления толкатель был неподвижен, то это означает, что скорость толкателя изменилась скачком, а ускорение теоретически равно бесконечности. Разрыв первой производной от функции является признаком жесткого удара. Следовательно, при линейном законе перемещения толкателя в начале и конце каждой фазы движения возникают жесткие удары. Благодаря деформации звеньев кулачкового механизма ни ускорение, ни пропорциональные ему приведенные силы инерции практически не являются бесконечными. Однако закон линейного перемещения толкателя используют только в тихоходных кулачковых механизмах.

Двойной гармонический закон перемещения толкателяиспользуется в быстроходных кулачковых механизмах. На фазе удаления имеем

. (6.44)

Закон (6.44), синусоидальный закон (6.1) и все полигармонические законы движения толкателя внутри фазовых углов вращения кулачка относятся к безударным законам.

Сравнить законы движения толкателя между собой можно по максимальным значениям аналогов ускорений. Пусть закон движения симметричный, фазовый угол равен j_уд, ход толкателя равен h. Согласно симметричному закону постоянных ускорений, максимальное значение аналога ускорений при k =1 на основании (6.27) будет равно , для линейно-убывающего закона на основании (6.16) имеем , а для закона с линейно-возрастающими аналогами ускорений с учетом (6.31) .Таким образом, при одинаковой частоте вращения кулачка максимальное ускорение толкателя при линейно-убывающем законе в 1,5, а при линейно-возрастающем в 6 раза больше, чем при постоянных ускорениях.

Вышеперечисленные законы движения относятся к простейшим законам движения толкателя внутри фаз. Дополнительные сведения о законах движения можно получить из специальной литературы и учебников [1], [4].