Пример 1. Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2x² + 2y² – 8x + 5y – 4 = 0.

Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x² + y² – 4x + 2,5y – 2 = 0

x² – 4x + 4 –4 + y² + 2,5y + 25/16 – 25/16 – 2 = 0

(x – 2)² + (y + 5/4)² – 25/16 – 6 = 0

(x – 2)² + (y + 5/4)² = 121/16

Отсюда находим О(2; -5/4); R = 11/4.

7.1.2 ЭЛЛИПС

Эллипсом называется линия, заданная уравнением .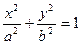

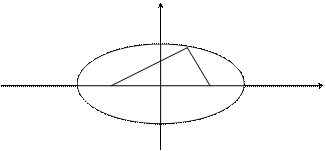
Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

М

r₁

r₂

F₁ O F₂ х

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема Фокусное расстояние и полуоси эллипса связаны соотношением:

a² = b² + c².

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Е = с/a.

Т.к. с < a, то е < 1.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a/e; x = -a/e.