 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
ЗАДАНИЕ N 5. Эксцентриситет гиперболы равен
|
|
Эксцентриситет гиперболы равен 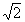 . Составить простейшее уравнение гиперболы, проходящей через точку М(
. Составить простейшее уравнение гиперболы, проходящей через точку М(
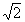 ).
).
Решение:
Согласно определению эксцентриситета, имеем  , или
, или  . Но
. Но  ; следовательно
; следовательно  , или
, или  , т.е. гипербола равнобочная.
, т.е. гипербола равнобочная.
Другое равенство получим из условия нахождения точки М на гиперболе, т.е.
 , или
, или  . Поскольку
. Поскольку  , получим
, получим  , т.е.
, т.е. 
Таким образом, уравнение искомой гиперболы имеет вид 
САМОСТОЯТЕЛЬНАЯ РАБОТА 7
ЗАДАНИЕ N 1
Тема: Кривые второго порядка
Известно, что уравнение параболы имеет вид  Тогда уравнением параболы, изображенной на чертеже,
Тогда уравнением параболы, изображенной на чертеже,  является …
является …
1. 
2. 
3. 
4. 
ЗАДАНИЕ N 2
Тема: Кривые второго порядк
Известно, что уравнение параболы имеет вид  Тогда уравнением параболы, изображенной на чертеже, является …
Тогда уравнением параболы, изображенной на чертеже, является …
 1.
1. 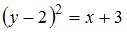
2. 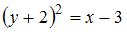
3. 
4. 
ЗАДАНИЕ N 3
Тема: Кривые второго порядка
Уравнением окружности, изображенной на чертеже,
является …1. 
2. 
3. 
\4. 

ЗАДАНИЕ N 4
Тема: Кривые второго порядка
Уравнением эллипса, изображенного на чертеже,

является …
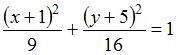


ЗАДАНИЕ N 5
Тема: Кривые второго порядка
Известно, что уравнение параболы имеет вид  Тогда уравнением параболы, изображенной на чертеже,
Тогда уравнением параболы, изображенной на чертеже,

является …
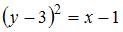



Дата публикования: 2014-11-03; Прочитано: 755 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
