Гипербола

Рассмотрим еще одну кривую второй степени - гиперболу.

Гиперболой называется геометрическое место точек, разность расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная.

Эта постоянная должна быть положительной и меньше расстояния между фокусами. Очевидно, что она не может быть больше расстояния между фокусами; если же она равна этому расстоянию, то рассматриваемое геометрическое место состоит из тех точек прямой, проходящей через фокусы, которые лежат вне отрезка, соединяющего фокусы.

Геометрическим местом точек, для которых указанная разность равна нулю, является перпендикуляр, проведенный к отрезку, соединяющему фокусы, в его середине.

Обозначим разность, упомянутую в определении гиперболы, через расстояние между фокусами через и выберем оси координат также, как и при рассмотрении эллипса. Пусть 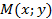- произвольная точка гиперболы.

По определению гиперболы . В правой части этого равенства надо взять знак плюс, если , и знак минус, если .

Так как , то это равенство можно записать в виде: = 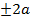. Это и есть уравнение гиперболы в выбранной системе координат.

Освобождаясь в этом уравнении от радикалов, аналогично тому, как это делалось при рассмотрении эллипсов, можно привести это уравнение к виду

Так как , то величина положительная. Обозначим ее через 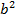, тогда уравнение (4.32) примет форму

Это уравнение гиперболы называется каноническим. Ему удовлетворяют любые ее точки и только они.

Так как уравнение (4.33) содержит только квадраты текущих координат, то оси координат являются осями симметрии гиперболы. Ось симметрии гиперболы, на которой располагаются фокусы, называется фокальной осью. Точка пересечения осей симметрии - центр симметрии - называется центром гиперболы.

y

0

x

Рис.4.14. Гипербола.

Найдем точки пересечения гиперболы с осями симметрии - вершины гиперболы. Полагая в (4.33) , найдем абсциссы точек пересечения гиперболы с осью абсцисс:

, откуда и .

Следовательно, точки и являются вершинами гиперболы (рис.4.14), расстояние между ними равно Чтобы найти точки пересечения с осью ординат, положим в (4.33) . Для определения ординат этих точек получим уравнение

, откуда и ,

т. е. для 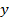мы получили мнимые значения; это означает, что ось 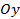не пересекает гиперболы. В соответствии с этим ось симметрии, пересекающая гиперболу, называется действительной осью симметрии (фокальной осью); ось симметрии, которая не пересекает гиперболу, называется мнимой осью симметрии.

Чтобы более ясно представлять себе вид гиперболы, рассмотрим две прямые, тесно с ней связанные - ее асимптоты.

Предполагая 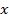и 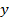положительными, решим уравнение (4.33) относительно ординаты 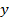, получим:

Сопоставим (4.34) с уравнением прямой Найдем

Таким образом, мы доказали, что с ростом 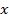гипербола неограниченно приближается к прямой . То же будет иметь место при движении точки 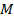по гиперболе в третьем квадранте. Наконец, в силу симметрии гиперболы относительно оси ординат, мы получим вторую прямую , симметрично расположенную с прямой , к которой также будет неограниченно приближаться точка 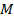при движении по гиперболе и удалении от начала координат (во втором и четвертом квадрантах).

Эти две прямые называются асимптотами гиперболы; они имеют уравнения

Очевидно, что асимптоты гиперболы проходят через диагонали прямоугольника, одна сторона которого параллельна оси абсцисс и равна 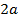, другая - параллельна оси ординат и равна , а центр лежит в начале координат (рис.4.14).

Рассмотрим произвольную точку 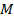гиперболы и фокальные расстояния 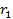и 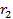этой точки до соответствующих фокусов. В силу определения

, (4.35)

где знак плюс относится к точкам правой ветви гиперболы, а знак минус - к левой. Учитывая (4.29), имеем:

, (4.36)

Перепишем это уравнение в виде и воспользуемся равенством (4.35), это нам даст

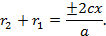
Решая последнее уравнение совместно с уравнением (4.35), получим выражения для и :

Величина 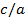называется эксцентриситетом гиперболы, обозначать ее будем через 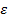. Очевидно, что 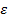есть отношение фокусного расстояния к длине действительной оси 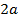, причем теперь 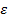>1, так как c>a.

Прямые , перпендикулярные к фокальной оси гиперболы и расположенные на расстоянии от ее центра, называются директрисами гиперболы, соответствующими правому и левому фокусам. Так как для гиперболы 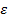>1, то <1 и, следовательно, директрисы располагаются между вершинами.

Легко показать, что отношение расстояний любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная, равная 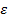. Оставляем доказательство этого факта читателю.

До сих пор мы рассматривали гиперболы с центром в начале координат, у которых действительной осью являлась ось абсцисс. Гипербола

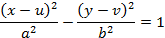
имеет центр в точке 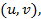а ее действительная ось проходит через эту точку и параллельна оси абсцисс. У гипербол же

действительной осью являются ось ординат и прямая, параллельная ей, соответственно; центр же первой гиперболы лежит в начале координат, а второй - в точке