Запись систем в матричной форме и их решение

Рассмотрим уравнение

,

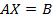где , , ║X 4ij 0║. Если элементы матриц 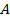и аданы, а элементы матрицы не известны, то написанное матричное равенство называется матричным уравнением. Пусть матрица 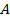имеет обратную матрицу . Умножая матричное уравнение слева на получим: или

,

что дает решение рассматриваемого матричного уравнения.

Рассмотрим снова систему (2.11). Ее коэффициенты при неизвестных составляют матрицу, которую мы будем обозначать буквой 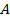и называть матрицей коэффициентов системы:

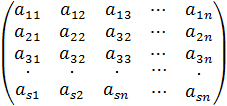
Введем в рассмотрение еще две матрицы - матрицы-столбцы

их элементами являются соответственно правые части уравнений системы (2.11) и неизвестные системы.

Рассмотрим произведение - это есть матрица - столбец, состоящая из одного столбца:

мы видим, что элементами этой матрицы являются левые части уравнений системы (2.11), тогда с учетом определения равенства матриц, мы можем утверждать, что равенство

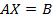, (2.16)

выполняется в том и только том случае, когда элементы матрицы (неизвестные системы (2.11)) принимают значения, удовлетворяющие системе (2.11) (являются ее решением).

Таким образом, система (2.11) эквивалентна, с точки зрения совпадения множества решений, матричному уравнению (2.16). Уравнение (2.16) называют матричной записью системы. Такая запись используется не только в целях упрощения обозначений, она полезна, так как позволяет привлекать аппарат теории матриц для решения и исследования систем линейных уравнений.

Если матрица 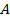системы (2.16) является квадратной (т.е. если число уравнений системы (2.11) равно числу ее неизвестных) и имеет обратную матрицу , то, умножая обе части равенства (2.16) слева на , получим:

, (2.17)

но , тогда из (2.17) следует, что

. (2.18)

Формула (2.18) позволяет находить решение системы (2.11), у которой число уравнений и неизвестных совпадают. Но для этого должна существовать матрица, обратная матрице коэффициентов системы, и, кроме того, необходимо эту матрицу вычислить. Решению этих и ряда других проблем служит определитель матрицы.