Пример 2.5

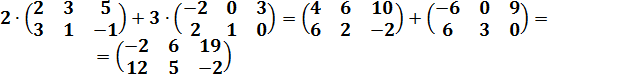
Рассмотрим еще одну операцию над матрицами - их произведение. Можно было бы произведение матриц определить по аналогии с их сложением, перемножая соответствующие элементы. Но такое умножение не находит серьезных применений. Определение произведения матриц, вводимое далее, не смотря на его кажущуюся сложность и непонятность, имеет глубокий смысл и связано с описанием линейных преобразований.

Произведением матрицы 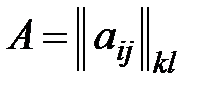на матрицу 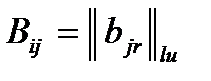называется матрица 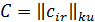(обозначается 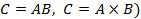, элемент 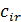которой равен сумме произведений соответствующих элементов строки 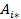матрицы 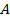на столбец 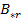матрицы :

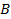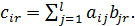(2.14)

Таким образом, чтобы вычислить элемент матрицы произведения, стоящий в i-ой строке и r-ом столбце необходимо взять i-ю строку первого сомножителя и "умножить" ее в соответствии с формулой (2.14) на r-й столбец второго сомножителя.

Отметим некоторые особенности введенной операции.

Умножение определено не для любых матриц, перемножать матрицы можно только если число столбцов матрицы - первого сомножителя, равно числу строк матрицы - второго сомножителя.

Уже из этого замечания следует, что произведение матриц не коммутативно, т.е. вообще говоря, не верно, что .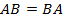

Число строк матрицы-произведения равно числу строк первого сомножителя, число столбцов - числу столбцов второго.

Произведение матриц ассоциативно, т.е.

?,

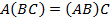при условии, что все указанные здесь произведения определены.