Логічні операції

Операція «НЕ» (інверсія, логічне заперечення, NOT). Нехай є деяке висловлювання А. Заперечення цього висловлювання позначається ` (прийнято читати: не А). Якщо висловлювання А правдиве (А = 1), то висловлювання неправдиве (` A = 0). Якщо висловлювання А неправдиве (А = 0), то висловлювання ` A правдиве ( = 1). Отже, для логічного заперечення справедливе таке правило:

= 1

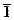= 0

Позначення операції в схемах логічних перетворень:

Операція «І» (кон’юнкція, логічне множення, AND). Операцію логічного множення двох змінних А і В позначають А Ù В (прийнято читати: А і В). Висловлювання А Ù В правдиве (А Ù В = 1) тільки в тому випадку, якщо одночасно правдиве А (А = 1) і правдиве В (В = 1). У всіх інших випадках це висловлювання неправдиве, тобто А Ù В = 0. Отже, при логічному множенні справедливе наступне правило:

0 Ù 0 = 0

0 Ù 1 = 0

1 Ù 0 = 0

1 Ù 1 = 1

Правило логічного множення справедливе не тільки для двох співмножників, але і для будь-якої їх кількості, тобто A Ù B Ù C Ù D Ù …. Позначення операції в схемах логічних перетворень:

Операція «АБО» (диз’юнкція, логічне додавання, OR). Операцію логічного додавання двох змінних А і В позначають А Ú В (прийнято читати: А або В). Висловлювання А Ú В правдиве (А Ú В = 1) в тому випадку, якщо хоча б одна із змінних А або В має значення правдиве (А = 1 або В = 1). Якщо ж ця умова не виконується, то висловлювання неправдиве (А Ú В = 0). Отже, при логічному додаванні справедливе наступне правило:

0 Ú 0 = 0

0 Ú 1 = 1

1 Ú 0 = 1

1 Ú 1 = 1

Правило логічного додавання справедливе не тільки для двох доданків, але і для будь-якої їх кількості, тобто A Ú B Ú C Ú D Ú …. Позначення операції в схемах логічних перетворень:

Операція «АБОіз виключенням» (додавання за модулем 2, нееквівалентність, XOR (Exclusive OR) ). Операція “АБО із виключенням” над двома змінними А і В позначають А В. Висловлювання А В правдиве (А В = 1) в тому випадку, якщо тільки одна із змінних А або В має значення правдиве (А = 1, В = 0 або А = 0, В = 1). Якщо ж ця умова не виконується, то висловлювання неправдиве (А В =0). Перша назва операції зумовлена тим, що результат даної операції збігається із результатом операції «АБО» за виключенням одного із чотирьох випадків – одночасної правдивості аргументів «виключається»). Друга назва – тим, що дійсно є складанням в кільці вирахувань за модулем 2. Третя назва – результат операції правдивий тільки тоді, коли значення операндів не співпадають. Отже, операція “АБО із виключенням” виконується за таким правилом:

0 0 = 0

0 1 = 1

1 0 = 1

1 1 = 0

Позначення операції в схемах логічних перетворень:

На основі розглянутих логічних висловлювань можна уявити будь-яке складне висловлювання, тобто будь-який логічний зв’язок можна виразити за допомогою логічних операцій додавання, множення і заперечення.

Операції «І», «АБО» і «АБО із виключенням» є не тільки комутативними, але і асоціативними, і тому легко узагальнюються на випадок кількох аргументів.

Інші логічні (бінарні, двійкові) операції:

Операція «АБО–НЕ» (стрілка Пірса, NOR) – двомісна логічна операція, введена в розгляд Ч. Пирсом [Чарльз Сандерс Пирс; дата нар. 10.09.1839, американський філософ, логік, математик, основоположник прагматизму і семіотики]. Операцію «АБО–НЕ» над двома змінними А і В позначають А ↓ В. Її результатом є інвертований результат операції «АБО». Операція «АБО–НЕ” виконується за таким правилом:

0 ↓ 0 = 1

0 ↓ 1 = 0

1 ↓ 0 = 0

1 ↓ 1 = 0

Висловлювання А ↓ В прийнято читати «ні А, ні В». Позначення операції в схемах логічних перетворень:

Стрілка Пірсу має ту властивість, що через її одну виражаються всі інші логічні операції. Наприклад, висловлювання (не A) еквівалентно висловлюванню А ↓ A, кон’юнкція A Ù B висловлювань A і B виражається так: (А ↓ A)↓(В ↓ В), диз’юнкція А Ú В еквівалентна (А ↓ В)↓(А ↓ В).

Операція «І–НЕ» (штрих Шеффера, NAND) [Джонатан Шеффер; нар. в 1957 р. в Торонто, Канада; дослідник теорії ігор] – є результатом інвертування результату операції «І», видає значення 0 тільки коли обидва операнди 1. Операцію «І–НЕ» над двома змінними А і В позначають А | В і виконуєть за таким правилом:

0 | 0 = 1

0 | 1 = 1

1 | 0 = 1

1 | 1 = 0

Позначення операції в схемах логічних перетворень:

Операція імплікація («якщо–то»). Операцію «якщо–то» над двома змінними А і В позначають А Ì В (іноді А → В). Результат співпадає з результатом операції «АБО» з інвертованим першим аргументом, видає значення 0 тільки коли перший операнд дорівнює 1 а другий – 0. Дана операція не є комутативною, на відміну від всіх вищеописаних бінарних операцій. Її можна розуміти як арифметичне ≤ (менше або рівно). Операція «якщо–то” виконується за таким правилом:

0 Ì 0 = 1

0 Ì 1 = 1

1 Ì 0 = 0

1 Ì 1 = 1

А – антецедент (передуючий), В –консеквент (подальший). Імплікація неправдива тоді і тільки тоді, коли антецедент правдивий, а консеквент неправдивий. Отже, «з правди не може випливати неправда!».

Операція еквіваленція. Еквіваленцією двох висловлювань А і В називається таке висловлювання, яке правдиве тоді і тільки тоді, коли обидва ці висловлювання А і В правдиві або обидва неправдиві, тобто видає 1 якщо і тільки якщо обидва аргументи рівні між собою. Є результатом інвертування результату операції «АБО із виключенням». Позначають операцію символом «Û». Операція виконується за таким правилом:

0 Û 0 = 1

0 Û 1 = 0

1 Û 0 = 0

1 Û 1 = 1

При розробці вузлів МП-систем значення неправдивого або правдивого висловлювання А, В, С до уваги не приймається; апарат алгебри логіки використовується для виконання заданих логічних перетворень. Наприклад, арифметичні перетворення (складання, віднімання) задаються у вигляді сукупності логічних перетворень над аргументами.