Додаткова інформація

Арифметичні операції над двійковими числами відрізняються простотою і легкістю технічного виконання. Приклади:

Додавання:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10 – відбувається переніс одиниці в старший розряд

Віднімання:

0 – 0 = 0

1 – 0 = 1

1 – 1 = 0

10 – 1 = 1 – відбувається позичка одиниці в старшому розряді

Множення:

0 ´ 0 = 0

0 ´ 1 = 0

1 ´ 0 = 0

1 ´ 1 = 1

1 ´ 1 = 1

В двійково-кодованих системах числення кожна цифра числа уявляється в двійковій системі числення.

16-кова і 8-кова системи числення є допоміжними системами при ручному записі. Зручність їх використання в тому, що запис числа коротший, а перетворення числа (“ 2 ” «“ 8 ”, “ 2 ” «” 16 ”) нескладне – кожна цифра 8- або 16-кового числа записується як двійкове число відповідно наведеним таблицям

При записі двійкового числа у 16-ковій (8-ковій) системі числення число розбивається ліворуч і праворуч від коми на четвірки (трійки) цифр і кожна тетрада (тріада) двійкових цифр записується як одна 16-кова (8-кова) цифра.

Приклади:

A5,2B₁₆ Û 1010 0101,0010 1011₂.

123,56₈ Û 001 010 011,101 110₂;

Таблиця 2. Таблиця відповідності 16- та 8-кових цифр і двійкових комбінацій

16-кова цифра	2-кова комбінація	16-кова цифра	2-кова комбінація		8-кова цифра	2-кова комбінація
		A
		B
		C
		D
		E
		F

Двійкове число або закодоване керуюче “слово” в МП-системах представляються набором цифр (1 і 0). У цифрових пристроях коди представляються у вигляді двох різних рівнів напруг або струму або у вигляді імпульсів. Один рівень або наявність імпульсу означає 1; інший рівень або відсутність імпульсу 0.

0 і 1 можуть відрізнятися також напрямом або імпульсами протилежного знаку. У МП-схемах змінні і відповідні ним сигнали змінюються не безперервно, а лише в дискретні моменти часу t=0, 1, 2, …, i, ….

Часовий інтервал між двома сусідніми моментами дискретного часу називається тактом або періодом представлення інформації.. Дискретний час можна представити сукупністю пронумерованих точок на осі часу, відповідних послідовним тактовим моментам. Часові інтервали між періодами представлення інформації можуть бути довільними.

Практично у всіх випадках МП-системи містять спеціальний блок, що виробляє тактові синхронізуючі імпульси (СІ), що відмічають моменти дискретного часу.

У цифрових пристроях застосовують потенційний і імпульсний способи представлення інформації.

При потенційному способі (рис. 2-а) 0 і 1 відповідають низька U ₀ і висока U ₁ напруги в певній точці схеми (потенційний код).

При імпульсному способі (рис. 2-б) 1 і 0 відповідають наявність і відсутність електричного імпульсу в певній точці схеми (імпульсний код).

Схеми МП-систем відповідно до типу сигналів, що використовуються для представлення інформації прийнято ділити на імпульсні, потенційні і імпульсно-потенційних. У перших схемах використовуються тільки імпульсні сигнали, у других – тільки потенційні, а в третіх – і ті і інші.

Для представлення і передачі кодів двійкових слів, які складаються з кількох двійкових розрядів, застосовують послідовний і паралельний способи (послідовний і паралельний коди).

Часові діаграми потенційного (а) та імпульсного (б) сигналів

Послідовні імпульсний (а) і потенційний (б) коди.

При послідовному способі кожний часовий такт використовується для відображення одного розряду слова, всі розряди якого передаються по одному каналу послідовно і фіксуються одним і тим же елементом. Номер розряду визначається номером такту, який відлічується від деякого нульового положення, співпадаючим з початком слова. Отже, двійковий код слова представляється у вигляді деякої часової послідовності потенційних або імпульсних сигналів, відповідних значенням цифр в розрядах слів.

На рисунку показані приклади послідовного імпульсного (рис. а) і послідовного потенціального кодів (рис. б), що з’являються дискретні моменти часу одночасно з синхроімпульсами (СІ).

При паралельному способі всі розряди двійкового коду слова передаються одночасно в одному часовому такті, фіксуються окремими елементами і проходять через окремі канали, кожний з яких призначений для представлення і передачі тільки одного розряду слова. При цьому код слова розгортається не в часі, а в просторі, так як значення цифр всіх розрядів слова передаються по кільком електричним колам одночасно (кількість кіл збігається числу розрядів).

Пристрої МП-систем в залежності від коду, що застосовується, називають пристроями послідовної або паралельної дії.

Для досягнення високої швидкодії основні пристрої МП-систем будуються паралельними. Однак вони вимагають більшої кількості апаратури, ніж пристрої послідовної дії, оскільки при паралельному коді треба мати стільки шин, а також запам’ятовуючих і перетворюючих елементів, скільки розрядів в слові. Тому в деяких пристроях застосовують послідовно-паралельний код, при якому слова розбиваються на «склади». «Склади» передаються, а іноді і обробляються послідовно. При цьому кожний «склад» передається паралельним кодом.

Значення одного двійкового розряду називається бітом. З точки зору інформатики – це мінімальний обсяг інформації, яку можна зберігати, обробляти і передавати (відповідь на питання: “так чи ні?”). Як правило, обробка інформації здійснюється по-байтно або в обсягах, кратних байту. Байтом називається вісім суміжних двійкових розрядів. Похідні від цієї одиниці використовуються для визначення місткості запам’ятовуючих пристроїв:

1 Кбайт = 1024 байт;

1 Мбайт = 1024 Кбайт;

1 Гбайт = 1024 Мбайт.

Вічка постійних і оперативних запам’ятовуючих пристроїв, де зберігаються байти, визначаються номером (адресою).

Для представлення чисел і командних слів в МП-системах використовується один або кілька байтів.

Числа в МП-системах можуть бути представлені у формі з фіксованою або плаваючою крапкою.

Фіксована форма запису – це звична для нас форма, в якій положення крапки, що відділяє цілу частину числа від дробової, фіксується в певному місці відносно розрядів числа. Звичайно мається на увазі (тобто спеціально не позначається), що крапка знаходиться або перед старшим розрядом, або після молодшого. В першому випадку це дробові числа, а в другому – цілі числа.

Якщо крапка фіксована перед старшим розрядом, то по абсолютному значенню числа можна представити в діапазоні 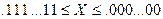, що відповідає десятковим значенням 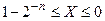(n – число розрядів).

Якщо крапка фіксована після молодшого розряду, то в десятковому зображенні числа можуть бути представлені в діапазоні 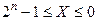. Якщо значення чисел перевищує верхню межу діапазону, то говорять, що сталося переповнення розрядної сітки.

Перевага форми представлення чисел з фіксованою крапкою в тому, що її застосування значно спрощує логічні і керуючі схеми МП. Це обумовлено тим, що арифметичні і інші операції здійснюються значно простіше, ніж при застосуванні форми з плаваючою крапкою. Наприклад, можна складати і віднімати числа без попереднього вирівнювання їх порядків, так як всі однойменні розряди всіх чисел займають постійні і однакові позиції.

Однак при підготовці задач до розв’язання необхідно слідкувати за тим, щоб перед додаванням або відніманням вихідні числа мали однакові масштаби. Крім того, треба слідкувати за можливими значеннями проміжних результатів і через підбір масштабу виключати переповнення розрядної сітки.

Представлення чисел у формі з фіксованою крапкою широко застосовується в спеціалізованих МП і МП-системах, де коло задач є наперед визначеним і можливо врахувати діапазон зміни чисел.

Для представлення чисел у формі з фіксованою крапкою використовується один або кілька байтів. На рис. (а) показана розрядна сітка дробових чисел у вигляді 4-байтного (32 біти) слова, включаючи знак перед старшим розрядом. Розряді пронумеровані зліва направо. Для кодування знаку використовується “знаковий” розряд в цьому розряді 0 відповідає плюсу, а 1 – мінусу. На розрядній сітці вказана вага кожного розряду. Діапазон додатних чисел, представлених в цій розрядній сітці, дорівнює 0 £ Х £ 1– 2^–31.

Представлення двійкового числа у формі з фіксованою крапкою.

а – числа по модулю менше 1; б – цілі числа.

На рис. (б) показана розрядна сітка для представлення 32-розрядних цілих чисел, включаючи знак. В цьому випадку діапазон представлення додатних чисел дорівнює 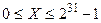, що відповідає діапазону абсолютних десяткових чисел приблизно від 0 до 2,15´10 ⁹.

Використання формату з фіксованою крапкою дозволяє підвищити швидкодію МП-системи, оскільки операції з такими числами виконуються швидше.

Представлення чисел у формі з плаваючою крапкою. В МП-системах широкого застосування (наприклад, персональних комп’ютерах) основна форма представлення чисел – з плаваючою крапкою. В цьому випадку число записується в розрядну сітку у вигляді двох груп цифр. Одна група відповідає порядку числа, друга – мантисі. Для зображення чисел використовується формульна залежність X=q ^p ´ M, де q – основа системи числення; p – порядок числа (ціле число) M – мантиса числа (дробове число). Так наприклад, у 10-вій системі числення число 1234,567 по цій формулі можна представити як 10⁴´0,1234567; 0,0009876 = 10^-3´0,9876. Порядок р разом із знаком вказує дійсне положення крапки в числі Х.

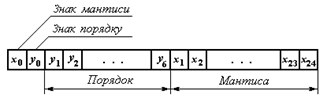
На рисунку показана розрядна сітка двійкового числа у формі з плаваючою крапкою. Мантиса числа менша за одиницю, її знак відповідає знаку числа. Значення порядку р, що уявляє ціле число, визначає положення крапки в числі. Із зміною порядку крапка немовби “плаває” в зображенні числа.

При представленні чисел у формі з плаваючою крапкою в МП-системах досягається широкий діапазон зображення чисел без застосування масштабних коефіцієнтів. Однак структура таких МП-систем значно ускладнюється, так як при виконанні операцій над числами з плаваючою крапкою необхідно мати окремі пристрої для виконання операцій як над мантисами, так і над порядками чисел. При цьому швидкість виконання операцій додавання і віднімання нижче, ніж в МП-системах з формою представлення чисел з фіксованою крапкою, що пояснюється необхідністю проведення додаткових дій по нормалізації чисел, вирівнюванню порядків і т.д.

Для спрощення операцій над порядками їх зводять до дій над цілими додатними числами, використовуючи уявлення чисел із зміщеним порядком. Для цього при записі чисел до їх порядків додається додатне число N = 2 ^k , де k – кількість розрядів, що відводяться на порядок. Це дозволяє при виконанні арифметичних дій над порядком код знаку порядку вважати старшим розрядом числа, що визначає порядок.

При зображенні з порядком одне і теж число може бути представлене з різними порядками (0,0009876 = 10^-3´0,9876 = 10 ^-4´9,876 = 10 ^-2´0,09876 = …). Для ліквідації подібної неоднозначності представлення чисел їх приводять завжди до нормалізованого виду, при якому старші розряди мантиси завжди повинні бути значущими. Нормалізований вид числа в наведеному вище прикладі виділений шрифтом.

Приведення числа до нормалізованого виду називається нормалізацією. Для нормалізації будь-який зсув мантиси на розряд відповідає зменшенню або збільшенню на одиницю порядку в залежності від зсуву мантиси вправо чи вліво.

В МП-системах, іноді, передбачено використання двійково-десяткового коду. В двійково-десятковому коді десяткові цифри числа від 0 до 9 представляються 4-розрядними двійковими комбінаціями від 0000 до 1001, тобто двійковими еквівалентами десяти перших 16-кових цифр (див. табл. 2). Коди від 1010 до 1111 не можуть використовуватись як цифри і використовуються як коди знаку числа: коди 1011 і 1101 представляють знак мінус, інші коди 1100 і 1010 – знак плюс. Вибір кодів знаків залежить від вибору системи кодування. Перетворення з двійково-десяткової системи в десяткову (і зворотнє перетворення) виконується шляхом прямої заміни чотирьох двійкових цифр однією десятковою цифрою (або зворотньою заміною). Дві двійково-десяткові цифри складають 1 байт. Десяткове число може займати в двійково-десятковому кодуванні один і більше байтів. Складання двійково-десяткових чисел, що мають один десятковий розряд, виконується так же, як і складання 4-розрядних двійкових чисел без знаку, за винятком того, що при отриманні результату, що перебільшує 1001, необхідно робити корекцію. Результат коректується через додавання двійкового коду числа 6, тобто коду 0110. Якщо первинне двійкове додавання або додавання коректуючого числа призводить до виникнення переносу, то при складанні багаторозрядних двійково-десяткових чисел здійснюється переніс в наступний десятковий розряд.