 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные алгебры
|
|
Азн 16.16. Линейной алгеброй над полем Р называется множество А, когда над А заданы операции сложения, умножения, а также заданное умножение элементов из А на скаляры (элементы из Р) и при этом выполняются следующие условия: 1) А относительно сложения и умножения элементов из А является кольцом; 2) А относительно сложения элементов из А и умножения на скаляр является линейным пространством; 3) Умножение элементов из А и умножение на скаляр удовлетворяют следующему условию:
 P
P  A
A 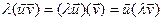 .
.
Прыклад 16.17. 1) С над R. 2) Mat(n´n:P). 3) P[x].
Св-во.16.18. Если V – линейное пространство над Р, то End(V) – лінейная алгебра над Р. Доказательство. То, что выполняется пункт 1 из определения 16.16 доказано в 16.10, пункт 2 из определения 16.16 выполняется по 16.15. Осталось доказать, что выполняется условие 3.  P
P  ÎEnd(V)
ÎEnd(V) 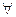
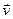 Î V
Î V
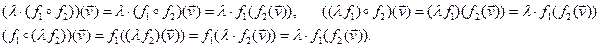
Из равенства правых частей следует равенство, которую надо доказать.■
Инвариантные подпространства. Собственные векторы. Простейшие свойства
Азн.16.1. f ÎEnd(V). Подпространство U пространства V называется инвариантной относительно f (или f - инвариантной), когда  Î U
Î U  Î U (1)
Î U (1)
Прыклад 16.2.1. V =V2, prx – проекция на ось Ox. U 1=R  R} - инвариантная относительно prx подпространство, так как
R} - инвариантная относительно prx подпространство, так как  R,
R,  U 1. U 2=R
U 1. U 2=R  R} - также инвариантные относительно prx подпространство, так как
R} - также инвариантные относительно prx подпространство, так как 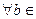 R,
R, 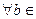 R
R  U 2.
U 2. 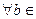 R
R  U 2.
U 2.
16.2.2. V = V3, f – поворот вокруг оси Oz на угол  . f - инвариантными являются U z і U xoy - просторо векторов плоскости xOy.
. f - инвариантными являются U z і U xoy - просторо векторов плоскости xOy.
16.2.3. Для оператора D деференцирования пространства P[x] для произвольного натурального n пространства
P n[x] является D-инвариантными.
16.2.4. Для произвольного f ÎEnd(V) подпространства  і V являются f - инвариантными. Они называются тривиальными.
і V являются f - инвариантными. Они называются тривиальными.
Св-во 16.3 Когда f ÎEnd(V), U 1 и U 2 f - инвариантные подпространства, тогда U 1  U 2 также f- инвариантное подпространство. Доказ. Рассмотрим
U 2 также f- инвариантное подпространство. Доказ. Рассмотрим 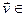 U 1
U 1  U 2 . То
U 2 . То 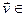 U 1 откуда следует, что
U 1 откуда следует, что  Î U 1. Аналогично,
Î U 1. Аналогично,  Î U 2, ■
Î U 2, ■
Азн. 16.4. Ненулевой вектор 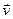 Î V называется собственным вектором оператора f ÎEnd(V), когда существует
Î V называется собственным вектором оператора f ÎEnd(V), когда существует  ÎP такой, что f
ÎP такой, что f 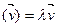 . При этом говорят, что
. При этом говорят, что  - собственная значимость линейного оператора f, которое соответствует вектору
- собственная значимость линейного оператора f, которое соответствует вектору 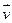 .
.
Прыклад 16.5. У линейного оператора prx линейного пространства V2 вектор  является собственным из собственной значимостью 1, поскольку
является собственным из собственной значимостью 1, поскольку  . Т.к.
. Т.к.  , вектор
, вектор  - собственный, которому соответствует собственная значимость 0.
- собственный, которому соответствует собственная значимость 0.
Св-во 16.6. Когда  - собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость
- собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость  ÎP, тогда для произвольного
ÎP, тогда для произвольного  ÎP\{0} вектор
ÎP\{0} вектор  также является собственным вектором оператора f, которому также соответствует собственная значимость
также является собственным вектором оператора f, которому также соответствует собственная значимость  . Доказ. По условию
. Доказ. По условию  . Тогда очевидно, что
. Тогда очевидно, что  і
і  .■
.■
Вынік 16.7 Когда  - собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость
- собственный вектор линейного оператора f ÎEnd(V), которому соответствует собственная значимость  , тогда подпространство P
, тогда подпространство P  ={
={ 

 ÎP} является f-инвариантной и каждый ненулевой вектор этого пространства является собственным вектором этого пространства является собственным вектором f, которому соответствует собственная значимость
ÎP} является f-инвариантной и каждый ненулевой вектор этого пространства является собственным вектором этого пространства является собственным вектором f, которому соответствует собственная значимость  . Доказ. Следует из 17.6 и того, что f
. Доказ. Следует из 17.6 и того, что f  .■
.■
Азн. 16.8 Пусть  (3) -базис пространства V, f ÎEnd(V) і А =
(3) -базис пространства V, f ÎEnd(V) і А =  – матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномам f называется полином
– матрица оператора f в базисе (3).Характеристическим полиномам матрицы А, а также характеристическим полиномам f называется полином
 (4).
(4).
Дата публикования: 2014-11-04; Прочитано: 233 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
