Ортогональные операторы и ортогональные матрицы

ОПР.14.1. Пусть ε – Евклидовое пространство. Лин. Преобразование f: ε ε наз. ортогональным, если Î ε .

Опр.14.5. Матрица A ÎMat(n´n;R) наз. ортогональной, если . Прыклад14.6.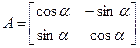

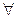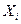Лемма 14.7. Если A, B ÎMat(n´n;R) і X, Y ÎRⁿ тады . Доказ. . Т.к , - любые, рассиотрим -столбец, у которого і -ы элемент равен 1, а все остальные 0. Так определим и трудно заметить, что . А это значит, что 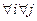, значит, .■

Св-во14.8. Ортогональный оператор Евклидового пространствав ортонормированном базисе имеет ортогональную матрицу. До-во. Пусть 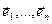ортанармированный базис ε ⁿ, f: ε ⁿ ε ⁿ - ортогональный оператор и А- его матрица в этом базисе. Рассмотрим произвольные векторы Î ε ⁿ, которые имеют столбцы координат , соответственно в данном базисе. Тогда векторы 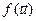і имеют столбцы координат і соответственно. Из ортогональностиf по 14.7 следует, что , Из леммы 15.6 следует, что .■

Св-во 14.10. Оператор f ортогонален тогда и только тогда, когда его матрица в ортонормированном базисе ортогональна. Доказательство: Утверждение, что если f – ортогонально, следует, что А – ортогональна (по 14.8.). Обратно: пусть есть ортонормированный базис, А – ортогональная матрица, тогда есть оператор f. Пусть в этом базисе имеют столбцы координат Х и Y. Тогда имеют столбцы координат АХ и AY. Тогда ■