Энергия магнитного поля. Рассчитаем энергию магнитного поля

Рассчитаем энергию магнитного поля. Для этого вычислим работу источника тока в цепи с индуктивностью. При установлении тока в такой цепи по закону Ома имеем

iR = ε 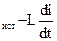. (63)

Умножив обе части равенства (63) на idt, получим i²Rdt = ε , или ,

то есть при установлении тока в цепи работа источника тока больше на .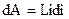

Если ток изменяется от нуля до некоторого стационарного значения I, то дополнительная работа равна . (64)

Эта работа равна изменению энергии магнитного поля. При выключении тока поле исчезает, и запасенная энергия проявляется в виде экстратоков.

Из приведенных рассуждений нельзя сделать заключение о том, где локализована эта энергия: в магнитном поле или самом проводнике. Опыты с электромагнитными волнами показывают, что энергия локализована в магнитном поле, поэтому она должна выражаться через основные характеристики поля или .

Считая, что вся работа источника тока, совершенная при создании магнитного поля, пошла на увеличение его энергии, и используя формулу индуктивности соленоида , получим из (63) .

Объективной характеристикой магнитного поля, не зависящей от геометрических факторов, является объемная плотность энергии w . (65)

Используя формулу связи между В и Н В=mm₀Н, выражение (65) можно представить в виде w 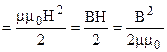. (66)

Таким образом, магнитное поле обладает энергией (66) и, как всякий материальный объект, должно характеризоваться массой и импульсом.

Используя формулу связи между массой и энергией Эйнштейна, w V, получаем массу единицы объема магнитного поля 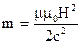и импульс единицы объема .