IV. Алгебра событий

Если множество – пространство элементарных событий, то любое случайное событие является его подмножеством. В случае, когда конечное или счетное множество любое подмножество – это событие. Но если – несчетное множество, случайными событиями являются не все подмножества, а только определенный класс подмножеств, который будет введен после определения операций над событиями. Событие – достоверное событие, а событие – невозможное событие.

1. Сумма событий. . Пример. Диаграмма.

2. Произведение событий. . Пример. Диаграмма.

3. Разность событий. . Пример. Диаграмма.

4. Противоположное событие. , т.е. событие А не происходит. Пример. Диаграмма.

События А и В называются несовместными, если . Если 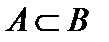,то наступление события А влечет за собой событие В. События А и В называются равными или равносильными (А=В), есл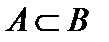и и .

Определение суммы и произведения событий переносится на бесконечную последовательность событий: , .

Свойства операций над событиями – это фактически свойства операций над множествами, т.к. а противоположное событие соответствует операции дополнения.

Определение 1.3. Класс подмножеств пространства элементарных событий называется алгеброй событий, если 1) , 2) (класс замкнут относительно операций). Если замкнут относительно бесконечных сумм и произведений, то класс называется –алгеброй (сигма–алгеброй).