Если А, (А ® В) - тавтологии, то тавтологией является В

Предположим, что В не является тавтологией. Тогда В принимает значение “ложь” при некотором наборе значений пропозиционных переменных. Но при этом же наборе значений переменных А имеет значение “истина”, так как А - тавтология (по условию). В таблице истинности такому набору значений А и В импликации (А® В) соответствует значение “ложь”. Получили противоречие с условием, что (А® В) - тавтология.

Если А - тавтология, содержащая пропозиционные переменные А1, А2,..., Аn, и В получается из А подстановкой формул Ф1, Ф2,..., Фn вместо А1, А2,..., Аn соответственно, то В есть тавтология, т.е. подстановка в тавтологию есть тавтология.

Доказательство: Обозначим А = А (А₁, А₂,..., А_n), тогда В символически запишется В = А (Ф₁, Ф₂,..., Ф_n ). Нам нужно показать, что 1) В - формула; 2) В - тавтология. Первое следует из определения формулы и из того, что Ф₁, Ф₂,..., Ф_n - формулы. Пусть задан некоторый набор значений для пропозиционных переменных формулы В. Формулы Ф₁, Ф₂,..., Ф_n примут тогда некоторые значениях₁, х₂,..., х_n (каждое х_k есть И или Л). Если мы придадим значения х₁, х₂,..., х_n соответственно пропозиционным переменным А₁, А₂,..., А_n, то значение А совпадет с истинностным значением В при заданном распределении значений пропозиционных переменных, входящих в В. Так как А по условию тавтология, то В при этом наборе значений переменных примет значение “истина”. Таким образом, В всегда принимает значение И, т.е. является тавтологией.

Пример 2. Формула F=(A®(B®A)) является тавтологией. Действительно, если предположить,что F принимает значение Л, то А - И, а (В® А) - Л. Но импликация (В ® ® А) принимает значение Л только в том случае, когда В - И, а А - Л. Получили противоречие с тем, что А - И. Рассмотрим формулы Ф₁ = С& A и Ф₂ = ((ùС)Ú А). Заменим в формуле F пропозиционную переменную А на Ф₁, а В на Ф₂, соответственно. Получим новую формулу F*= ((С& A) ® (((ùС)Ú А) ® (С& A))), которая является тавтологией. Убедимся в этом, составив для нее таблицу истинности.

А	С	(ù С)	((ù C) Ú A)	(С & A)	(((ù C) Ú A)®(C& A))	F*

Если в формуле F заменить только А на Ф₁, то получим еще одну тавтологию F** = = ((С& A) ® (B ® (С& A))).

А	В	С	(С& A)	(B ® (С& A))	((С& A) ® (B ® (С& A))).

Полные системы связок. В этом разделе мы рассмотрим множество логических связок с точки зрения взаимозаменяемости его элементов. Наша задача, выбрать такое минимальное подмножество, с помощью которого можно будет определить все остальные логические связки. Такое подмножество называется полным.

Определение 3. Две формулы F и Ф (F = Ф) называются логически эквивалентными (равносильными), если (F º Ф) - тавтология.

Из определения следует, что F равносильна Ф тогда и только тогда, когда в таблице истинности соответствующие столбцы совпадают.

Покажем, что формула (А ® В) равносильна формуле ((ùА) Ú В).

А	В	ùА	(А ® В)	((ùА) Ú В)

Равносильность (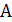 ® В) = ((ùА) Ú В) показывает, что связку ® можно исключить, заменив ее связками ù и Ú. Связку & можно исключить в силу равносильности (А & В) = (ù(ùА) Ú (ùВ)). Так как (А º В) = ((А ® В) & (В ® А)), а связки ® и & можно выразить через отрицание и дизъюнкцию, то связка º так же может быть исключена. Это показывает, что система связок { ù, Ú } полна.

Решение задач по теории множеств с помощью таблиц истинности. Если на выражения х Î А, у Î В посмотреть как на элементарные высказывания, то каждая формула теории множеств может быть заменена формулой логики высказываний. Это позволяет метод таблиц истинности применить к решению задач по теории множеств. Сведем этот способ решения задач к таблице.

Формулы теории множеств	Формулы логики
А È B А Ç В А \ В А D В = (А \ B) È(B \ A)	А Ù В А Ú В ù(A ® B) ù(A ® B) Ú ù(B ® A)

Например, докажем равенство (`А È В) = (А \ В). Переведем это равенство в доказательство равносильности формул ((ùА) Ú В) = (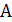 ® В), для чего воспользуемся таблицей истинности на предыдущей странице, показывающей их равносильность.