Решение. Окружности пересекаются по одну сторону относительно хорды

Окружности пересекаются по одну сторону относительно хорды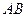

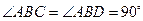
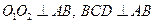
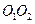- средняя линия треугольника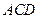

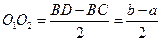
Окружности пересекаются по разную сторону относительно хорды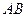

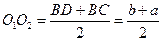
Ответ: 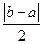или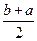

Задача 6.

В треугольнике 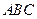на наибольшей стороне , равной 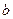, выбирается точка .

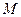Найдите наименьшее расстояние между центрами окружностей, описанных около треугольников 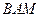и .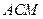

Решение.

Задача заслуживает уважения.

Выберем на стороне произвольным образом точку .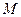

Докажем, что расстояние между центрами будет наименьшим, если эта точка является пересечением высоты, опущенной из вершины 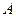на сторону .

Линия центров описанных около треугольников окружностей лежит на серединном перпендикуляре к стороне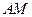

Хорда 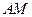является общей хордой при пересечении двух окружностей

Расстояние между центрами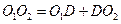

Отметим равные углы

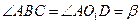и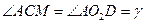

Отрезки линии центров 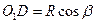и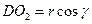

Чем меньше радиусы окружностей, тем меньше расстояние между центрами.

Радиус будет наименьшим, если центры окружностей лежат на сторонах треугольника: 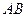и .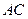

Тогда точка 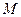является пересечением высоты 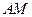, проведенной к стороне .

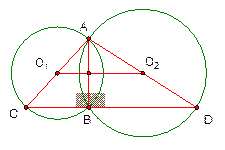
Треугольник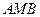и и - прямоугольные.

Центры окружностей лежат на серединах сторон.

Тогда 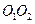- является средней линией треугольника с основанием

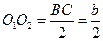
Изобразим полученную конфигурацию.

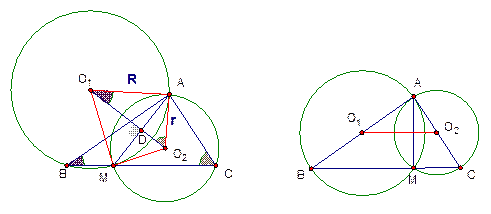
Ответ: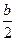

Тема 11.

Окружности, связанные с треугольником и четырехугольником.

Подготовительные задачи.

Задача 1.

Боковая сторона равнобедренного треугольника равна 2, угол при вершине равен .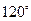

Найдите диаметр описанной окружности.