 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения
|
|
Напомним сначала, что корень 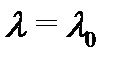 характеристического многочлена
характеристического многочлена 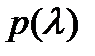 называется корнем кратности
называется корнем кратности 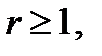 если
если
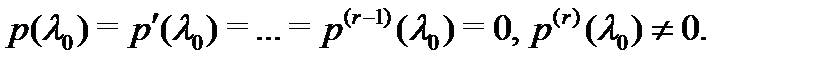
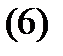
Полезно заметить, что если полином 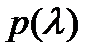 имеет
имеет 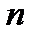 различных корней
различных корней  (
(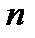 – степень многочлена
– степень многочлена 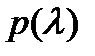 ), то все они имеют кратность
), то все они имеют кратность 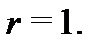 Однократные корни называют еще простыми корнями
Однократные корни называют еще простыми корнями 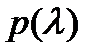 .
.
Записав для многочлена 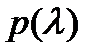 формулу Тейлора
формулу Тейлора
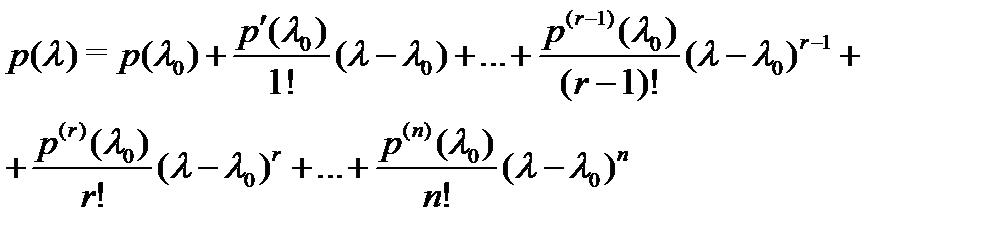
(остаточный член его равен тождественно нулю), получим с учетом равенств (6), что если 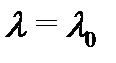 – корень кратности
– корень кратности 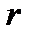 , то
, то  представляется в виде
представляется в виде
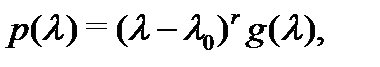
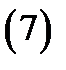
где 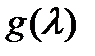 – многочлен степени
– многочлен степени 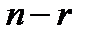 такой, что
такой, что 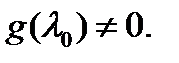 Очевидно, верно и обратное: если
Очевидно, верно и обратное: если 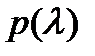 представляется в виде (7), где
представляется в виде (7), где  то
то 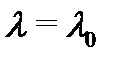 --- корень кратности
--- корень кратности 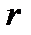 многочлена
многочлена 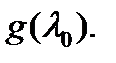
Построению фундаментальной системы решений в случае кратных корней характеристического уравнения  предпошлем несколько вспомогательных утверждений.
предпошлем несколько вспомогательных утверждений.
 Если
Если 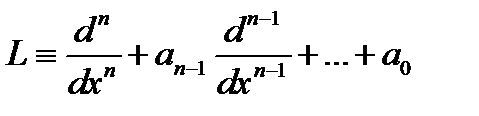 – дифференциальный оператор с постоянными коэффициентами
– дифференциальный оператор с постоянными коэффициентами 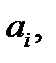 то имеет место формула
то имеет место формула
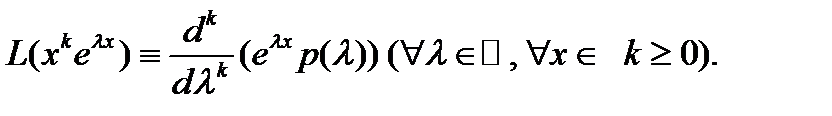
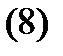
Действительно, по (2) имеем 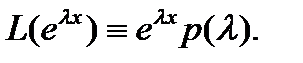 Дифференцируя это тождество по
Дифференцируя это тождество по 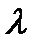 и учитывая, что операторы
и учитывая, что операторы 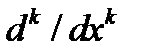 и
и 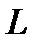 перестановочны при применении их к бесконечно дифференцируемой по
перестановочны при применении их к бесконечно дифференцируемой по 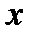 и
и 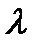 функции
функции 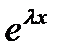 , будем иметь
, будем иметь
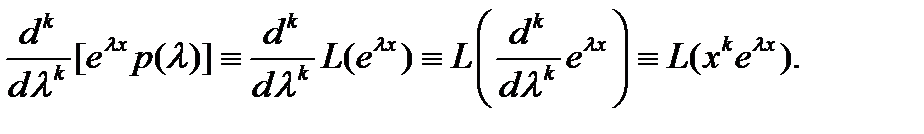
Таким образом, справедливо тождество (8).
 Пусть
Пусть 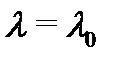 – корень кратности
– корень кратности 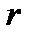 характеристического многочлена
характеристического многочлена 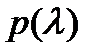 уравнения (21.26) с постоянными коэффициентами
уравнения (21.26) с постоянными коэффициентами 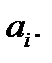 Тогда
Тогда 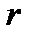 функций
функций
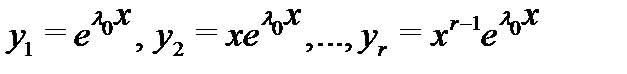
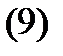
линейно независимы на любом отрезке 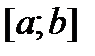 и являются решениями уравнения (1).
и являются решениями уравнения (1).
Доказательство. Пусть 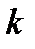 – любое натуральное число, удовлетворяющее неравенству
– любое натуральное число, удовлетворяющее неравенству 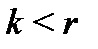 . Согласно
. Согласно  имеет место тождество
имеет место тождество

где 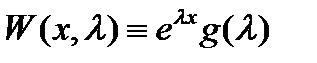 (см.
(см. 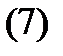 ). Имеем
). Имеем
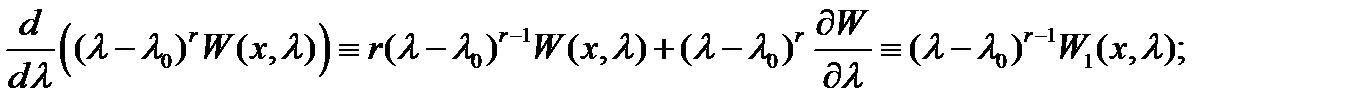
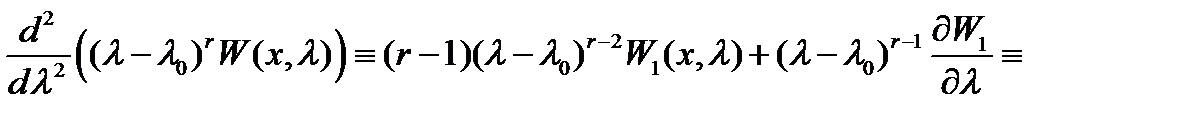

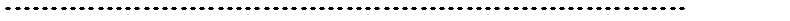
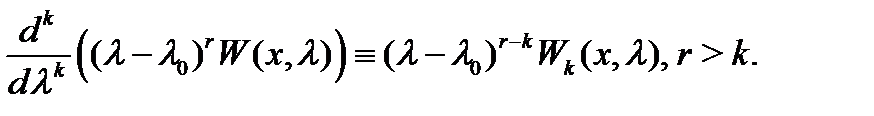
Полагая в последнем тождестве 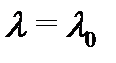 , будем иметь
, будем иметь
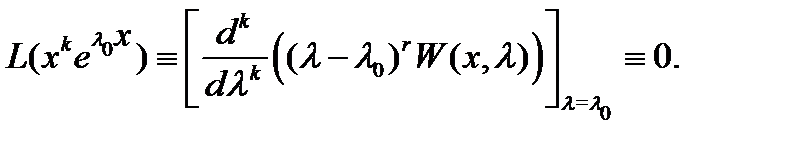
Это означает, что функции (9) являются решениями уравнения (1). Эти функции линейно независимы на любом отрезке 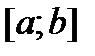 (см. утверждение
(см. утверждение 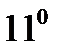 предыдущей лекции). Свойство
предыдущей лекции). Свойство 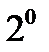 доказано.
доказано.
Если 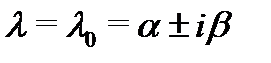 – комплексный корень кратности
– комплексный корень кратности 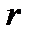 уравнения
уравнения  с постоянными и действительными коэффициентами
с постоянными и действительными коэффициентами  , то отделяя в (9) действительные и мнимые части, получаем
, то отделяя в (9) действительные и мнимые части, получаем 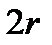 линейно независимых действительных решений
линейно независимых действительных решений
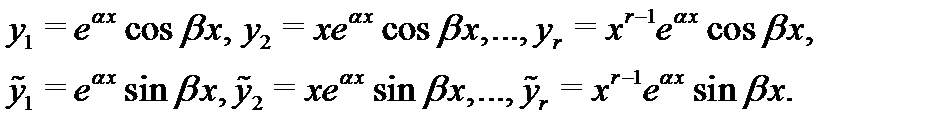
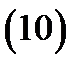
Из этого факта и предыдущих утверждений вытекает следующий алгоритм построения фундаментальной системы решений однородного уравнения (1) с постоянными и действительными коэффициентами 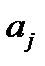 .
.
Дата публикования: 2014-11-04; Прочитано: 620 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
