 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм 1
|
|
1) По уравнению (1) составляем характеристическое уравнение  , заменив в (1) производные
, заменив в (1) производные 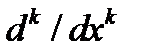 на степени
на степени 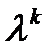 (
(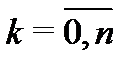 ).
).
2) Найдем корни 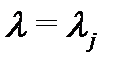 характеристического уравнения
характеристического уравнения  и установим их кратности.
и установим их кратности.
3) Каждому действительному корню 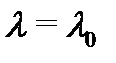 кратности
кратности 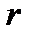 поставим в соответствие
поставим в соответствие  линейно независимых решений
линейно независимых решений 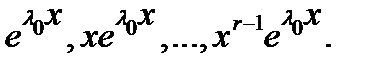
4) Каждой паре комплексно-сопряженных корней 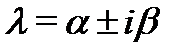 кратности
кратности 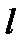 сопоставим
сопоставим 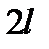 линейно независимых решений
линейно независимых решений
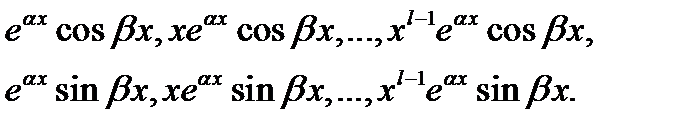
5) Объединим все полученные линейно независимые решения. Получим фундаментальную систему решений уравнения (1), состоящую из 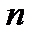 функций (
функций (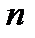 – порядок уравнения (1)).
– порядок уравнения (1)).
Общее решение уравнения (1) имеет вид
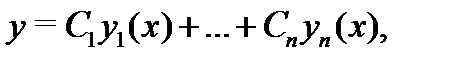
где 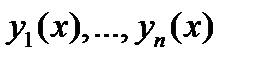 – построенная в алгоритме 1 фундаментальная система решений, а
– построенная в алгоритме 1 фундаментальная система решений, а 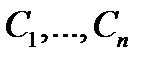 --- произвольные постоянные.
--- произвольные постоянные.
Пример 2. Найти общее решение уравнения 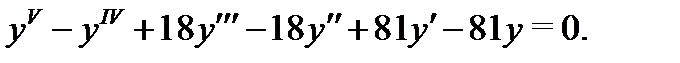
Решение. Составляем характеристическое уравнение  , находим его корни и устанавливаем их кратности:
, находим его корни и устанавливаем их кратности:
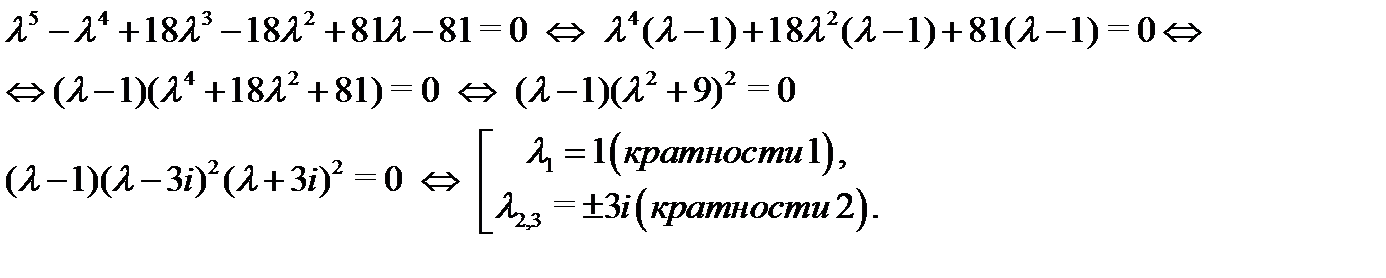
Согласно алгоритму 1 выписываем линейно независимые решения, отвечающие каждому корню:
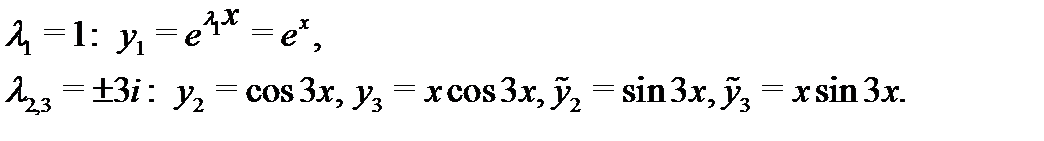
Следовательно, общее решение исходного уравнения имеет вид
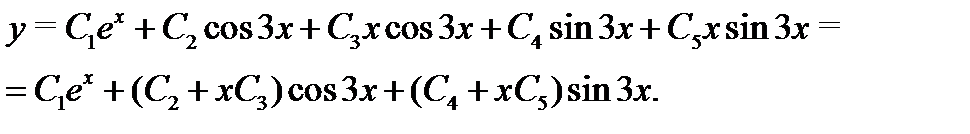
Дата публикования: 2014-11-04; Прочитано: 443 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
