Структура общего решения неоднородного уравнения. Метод вариации произвольных постоянных Лагранжа

Пусть дано неоднородное дифференциальное уравнение

Докажем следующее утверждение.

Теорема 1 (о структуре общего решения неоднородного уравнения). Если в уравнении (1) все коэффициенты и правая часть непрерывны на отрезке , то общее решение уравнения (1) (на этом отрезке) имеет вид

где 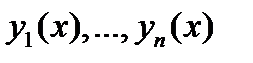– фундаментальная система решений соответствующего однородного уравнения а – частное решение неоднородного уравнения (1), произвольные постоянные.

Доказательство. Применяя оператор к функции (2), будем иметь

Это означает, что функция (2) является решением уравнения (1) при произвольных значениях постоянных . Пусть теперь --- произвольная точка в (). Покажем, что решение задачи Коши

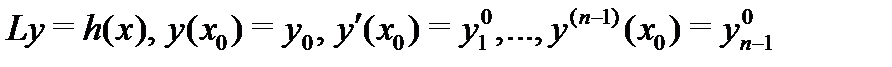
можно получить из (2) выбором определенных значений постоянных. Подчиняя (2) условиям (3), будем иметь

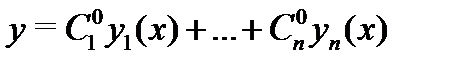Определитель этой системы совпадает с вронскианом в точке и поскольку фундаментальная система решений линейно независима на отрезке , то указанный определитель системы (4) не равен нулю. Следовательно, система (4) имеет единственное решение а значит функция является решением задачи Коши (3). Тем самым показано, что функция (2) является общим решением неоднородного уравнения (1). Теорема доказана.