Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения

Рассмотрим уравнение

с постоянными коэффициентами 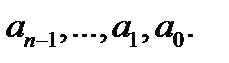Построим по нему алгебраическое уравнение

заменив в (1) производные на степени ().

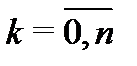Определение 1. Многочлен называется характерис-

тическим многочленом уравнения (1), а само уравнение – характеристическим уравнением, соответствующим уравнению (1).

Имеет место очевидное тождество

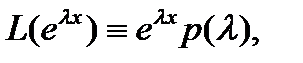
если – постоянная, так как

Теорема Эйлера. Для того чтобы экспонента ( – постоянная) была решением уравнения (1), необходимо и достаточно, чтобы было корнем характеристического многочлена (или, что то же самое, корнем характеристического уравнения ).

Доказательство. Действительно, если то из (2) следует тождество показывающее, что экспонента является решением уравнения (1). Обратно: если – решение уравнения (1), то и из (2) следует, что т.е. – корень характеристического многочлена Теорема доказана.

Из теоремы Эйлера сразу же вытекает следующий результат.

Теорема 1. Если все корни характеристического уравнения различны (т.е. ), то система функций

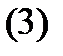
образует фундаментальную систему решений уравнения (1). В этом случае общее решение (на любом отрезке [a,b]) уравнения (1) имеет вид

где – произвольные постоянные.

Доказательство следует сразу из теоремы Эйлера и утверждения предыдущей лекции.

Общее решение (4) уравнения (1) может быть комплексным, если хотя бы один из корней характеристического полинома комплексный. Для уравнений (1) с действительными коэффициентами принято записывать общее решение в действительной форме. Это нетрудно сделать, если воспользоваться утверждением 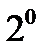лекции 4 и отделив в комплексном решении мнимую и действительную части: и Согласно действительные функции и также являются решениями однородного уравнения (1) с действительными коэффициентами. Поступив так с каждой комплексной экспонентой в , получим следующий результат.

Теорема 2. Пусть корни характеристического уравнения различны, а коэффициенты уравнения (1) действительны. Пусть, далее, корни –действительны, а остальные корни комплексны:

Тогда фундаментальную систему решений уравнения (1) можно выбрать в виде действительных функций

а общее решение уравнения (1) записать в виде

где – произвольные постоянные.

Доказательство следует из того, что функции (5) являются решениями уравнения (1) (лекция 4, утверждение ) и образуют линейно независимую систему на любом отрезке (лекция 4, утверждение ). Остаётся заметить, что в силу действительности всех коэффициентов уравнения (1) его характеристическое уравнение наряду с корнем имеет и комплексно-сопряженный корень

Пример 1. Найти общее решение уравнения

Решение. Составим характеристическое уравнение :

Разлагая его левую часть на множители, будем иметь

Итак, все корни характеристического уравнения различны. Согласно теореме 1 соответствующая фундаментальная система решений будет иметь вид

а значит общее решение исходного уравнения запишется в форме