 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения
|
|
Для неоднородного уравнения


с непрерывными на отрезке  коэффициентами
коэффициентами  и неоднородностью
и неоднородностью  был изложен метод вычисления частного решения
был изложен метод вычисления частного решения  называемый методом вариации постоянных. После того как найдено частное решение неоднородного уравнения, его общее решение вычисляется по формуле
называемый методом вариации постоянных. После того как найдено частное решение неоднородного уравнения, его общее решение вычисляется по формуле  где
где  общее решение соответствующего однородного уравнения
общее решение соответствующего однородного уравнения  Дадим еще один способ вычисления частного решения неоднородного уравнения (11), который применяется и в случае, когда коэффициенты этого уравнения переменные.
Дадим еще один способ вычисления частного решения неоднородного уравнения (11), который применяется и в случае, когда коэффициенты этого уравнения переменные.
 Пусть в уравнении (11) все коэффициенты
Пусть в уравнении (11) все коэффициенты  и правая часть
и правая часть  непрерывны на отрезке
непрерывны на отрезке  и пусть
и пусть 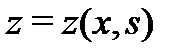 – решение соответствующего однородного уравнения
– решение соответствующего однородного уравнения  удовлетворяющее начальным условиям
удовлетворяющее начальным условиям

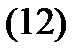
при любом фиксированном значении параметра  . Тогда частное решение неоднородного уравнения (21.22) с нулевыми начальными данными
. Тогда частное решение неоднородного уравнения (21.22) с нулевыми начальными данными  может быть записано в виде
может быть записано в виде


Доказательство. Найдем производные  функции (13), пользуясь формулой
функции (13), пользуясь формулой
С учетом начальных условий (12), будем иметь
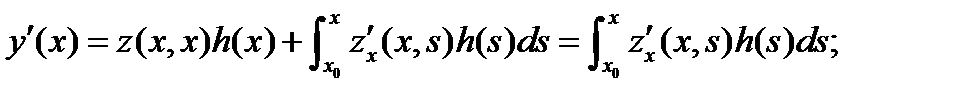

Следовательно,

так как  Таким образом, функция (13) удовлетворяет неоднородному уравнению
Таким образом, функция (13) удовлетворяет неоднородному уравнению  . Из выписанных выше равенств для производных функции (13) следует, что она удовлетворяет нулевым начальным условиям. Утверждение
. Из выписанных выше равенств для производных функции (13) следует, что она удовлетворяет нулевым начальным условиям. Утверждение  доказано.
доказано.
Пример 3. Найти общее решение неоднородного уравнения


где  – постоянная, а
– постоянная, а  – произвольная непрерывная на отрезке
– произвольная непрерывная на отрезке  функция.
функция.
Решение. Построим сначала общее решение соответствующего однородного уравнения  Так как его характеристическое уравнение
Так как его характеристическое уравнение  имеет два различных комплексно-сопряженных корня
имеет два различных комплексно-сопряженных корня  то его общее решение имеет вид
то его общее решение имеет вид
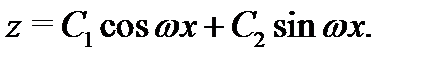
Подчиним это решение начальным условиям

Будем иметь


Итак,  , значит
, значит

Следовательно, частное решение неоднородного уравнения (14) имеет вид

а общее решение этого уравнения запишется в форме

Перейдем теперь к вычислению частного решения неоднородного уравнения (14) с помощью так называемого метода подбора. Оговоримся сразу же, что он применим для уравнений (11) с постоянными коэффициентами  и со специальной правой частью вида
и со специальной правой частью вида


где  и
и  – постоянные, а
– постоянные, а  и
и  --- многочлены степени
--- многочлены степени  и
и 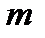 соответственно. Заметим, что функции вида
соответственно. Заметим, что функции вида

где  – многочлены, а
– многочлены, а  – постоянные (в общем случае комплексные), называются квазиполиномами (или квазимногочленами). Если выразить в (15)
– постоянные (в общем случае комплексные), называются квазиполиномами (или квазимногочленами). Если выразить в (15)  и
и  через экспоненты (см. предыдущую лекцию), то (15) можно представить в виде квазиполинома с комплексными коэффициентами. Поэтому функцию (15) будем также называть квазимногочленом. При этом будем считать, что числа
через экспоненты (см. предыдущую лекцию), то (15) можно представить в виде квазиполинома с комплексными коэффициентами. Поэтому функцию (15) будем также называть квазимногочленом. При этом будем считать, что числа  и
и  действительные, а число
действительные, а число  будем называть спектральным значением квазиполинома (15). Это число играет важную роль при построении частного решения неоднородного уравнения (11).
будем называть спектральным значением квазиполинома (15). Это число играет важную роль при построении частного решения неоднородного уравнения (11).
Алгоритм 2 (метода подбора)
Пусть требуется найти частное решение уравнения


с постоянными коэффициентами 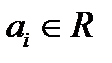 и с неоднородностью
и с неоднородностью  , являющейся квазимногочленом (15). Для этого надо сделать следующее:
, являющейся квазимногочленом (15). Для этого надо сделать следующее:
1) составить спектральное значение  правой части
правой части  уравнения (16);
уравнения (16);
2) если спектральное значение  не является корнем характеристического уравнения
не является корнем характеристического уравнения

то частное решение следует искать в виде


где  и
и 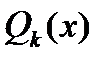 --- многочлены (с неопределенными коэффициентами) степени
--- многочлены (с неопределенными коэффициентами) степени  ;
;
3) если спектральное значение  является корнем кратности
является корнем кратности  хаpактеристического уравнения
хаpактеристического уравнения  , то частное решение следует искать в виде
, то частное решение следует искать в виде


где  и
и  – многочлены (с неопределенными коэффициентами) степени
– многочлены (с неопределенными коэффициентами) степени  ;
;
4) для вычисления неопределенных коэффициентов надо подставить функцию (17) (или (18)) в уравнение (16), сократить его обе части на экспоненту  и произвести приравнивание коэффициентов в обеих частях при одинаковых
и произвести приравнивание коэффициентов в обеих частях при одинаковых  а затем решить полученную линейную систему алгебраических уравнений относительно неопределенных коэффициентов.
а затем решить полученную линейную систему алгебраических уравнений относительно неопределенных коэффициентов.
Заметим, что если спектральное значение  является корнем характеристического уравнения
является корнем характеристического уравнения  , то говорят, что в уравнении (16) имеет место резонанс.
, то говорят, что в уравнении (16) имеет место резонанс.
Мы не будем заниматься обоснованием этого алгоритма. Такое обоснование можно найти во многих учебных пособиях по обыкновенным дифференциальным уравнениям (см., например, [I]). Покажем, как он работает на практике. Отметим, что при применении алгоритма 2 часто используется следующий принцип суперпозиции.
Принцип суперпозиции. Если правая часть  уравнения
уравнения


является линейной комбинацией непрерывных на отрезке 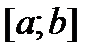 функций
функций  ,и если
,и если  решения уравнений
решения уравнений

то функция  является решением уравнения (19) (здесь числа
является решением уравнения (19) (здесь числа  могут быть и комплексными).
могут быть и комплексными).
Действительно, в силу линейности оператора  из тождеств
из тождеств

вытекает тождество

Рассмотрим несколько примеров.
Пример 4. Найти общее решение уравнения
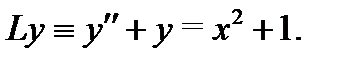

Решение. Так как в правой части (20) нет  , то
, то  и поскольку в правой части нет синусов и косинусов, то
и поскольку в правой части нет синусов и косинусов, то  . Значит, спектральное значение правой части равно
. Значит, спектральное значение правой части равно  Характеристическое уравнение
Характеристическое уравнение  имеет два различных чисто мнимых корня
имеет два различных чисто мнимых корня  и спектральное значение
и спектральное значение  oтличается от них, поэтому частное решение неоднородного уравнения (20) следует искать в виде
oтличается от них, поэтому частное решение неоднородного уравнения (20) следует искать в виде

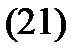
(т.е. в таком же виде, что и правая часть уравнения (20)). Для вычисления неопределенных коэффициентов  надо подставить (21) в (20) и произвести приравнивание коэффициентов при oдинаковых степенях
надо подставить (21) в (20) и произвести приравнивание коэффициентов при oдинаковых степенях  . Вычислим сначала производные от много-
. Вычислим сначала производные от много-
члена (21):  Значит,
Значит,  Приравнивание коэффициентов дает:
Приравнивание коэффициентов дает:


Подставляя найденные коэффициенты в (21), найдем окончательно частное решение неоднородного уравнения (20):  Поскольку корни
Поскольку корни  характеристического уравнения
характеристического уравнения  различны, то общее решение соответствующего однородного уравнения имеет вид
различны, то общее решение соответствующего однородного уравнения имеет вид  а значит общее решение исходного уравнения (20) запишется в форме
а значит общее решение исходного уравнения (20) запишется в форме 
Пример 5. Найти общее решение уравнения


Решение. Найти общее решение соответствующего однородного уравнения  не составляет труда, так как здесь корни характеристического уравнения
не составляет труда, так как здесь корни характеристического уравнения  различны:
различны:  Оно имеет вид
Оно имеет вид  Займемся вычислением частного решения неоднородного уравнения (22). Поскольку в правой части нет экспоненты
Займемся вычислением частного решения неоднородного уравнения (22). Поскольку в правой части нет экспоненты 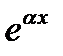 и синусов и косинусов, то спектральное значение
и синусов и косинусов, то спектральное значение 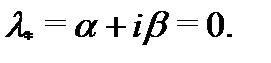 Оно является корнем характеристического уравнения кратности
Оно является корнем характеристического уравнения кратности  Согласно п.3 алгоритма 2 частное решение неоднородного уравнения (22) следует искать в виде
Согласно п.3 алгоритма 2 частное решение неоднородного уравнения (22) следует искать в виде


Вычисляя производные  функции (23) и подставляя ее в (22), будем иметь
функции (23) и подставляя ее в (22), будем иметь  Приравнивая здесь коэффициенты при одинаковых степенях
Приравнивая здесь коэффициенты при одинаковых степенях  получаем
получаем
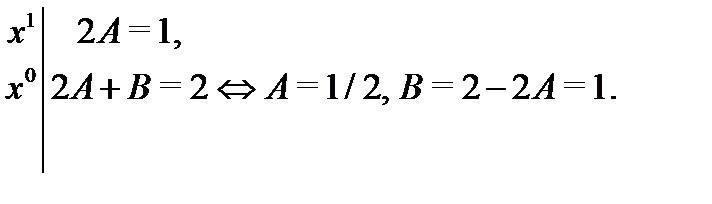
Подставляя 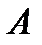 и
и  в (23), найдем частное решение уравнения (22) в виде
в (23), найдем частное решение уравнения (22) в виде  а значит, общее решение этого уравнения запишется в форме
а значит, общее решение этого уравнения запишется в форме

Пример 6. Решить уравнение


Решение. Спектральное значение правой части  равно
равно  , так как
, так как 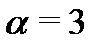 , а синусы и косинусы отсутствуют. Характеристическое уравнение
, а синусы и косинусы отсутствуют. Характеристическое уравнение  имеет два различных действительных корня:
имеет два различных действительных корня:  и
и  . Так как спектральное значение
. Так как спектральное значение  не является коpнем характеристического уравнения, то частное решение уравнения (24) следует искать в виде (см. п.2 алгоритма 2):
не является коpнем характеристического уравнения, то частное решение уравнения (24) следует искать в виде (см. п.2 алгоритма 2):


Для составления уравнений относительно неопределенных коэффициентов  и
и 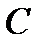 , найдем производные функции (25):
, найдем производные функции (25):

Следовательно,

Сокращая здесь экспоненту, получаем тождество

Приpавнивание коэффициентов дает:

Подставляя  ,
,  и
и  в (25), получаем частное решение в виде
в (25), получаем частное решение в виде 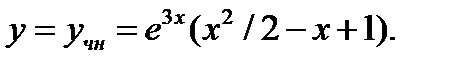 При этом общее решение соответствующего однородного yравнения строится по корням
При этом общее решение соответствующего однородного yравнения строится по корням  и
и  характеристического уравнения следующим образом:
характеристического уравнения следующим образом: 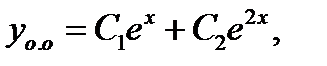 а значит, общее решение неоднoродного уравнения (24) запишется в виде
а значит, общее решение неоднoродного уравнения (24) запишется в виде
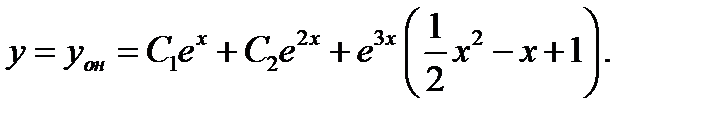
Пример 7. Построить общее решение уравнения
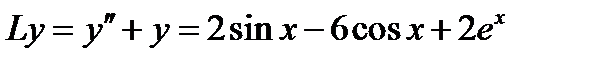
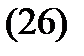
и найти его интегральную кривую, удовлетворяющую начальным условиям

Решение. Здесь правая часть не является квазиполиномом вида (17), поэтому сразу воспользоваться алгоритмом 2 нельзя. Разобьем уравнение (26) на два уравнения




к которым можно применить метод подбора. Если будут найдены частные решения  и
и  этих уравнений, то, согласно принципу суперпозиции, частное решение исходного уравнения (26) будет иметь вид
этих уравнений, то, согласно принципу суперпозиции, частное решение исходного уравнения (26) будет иметь вид 
Займемся поиском частного решения уравнения (27). Спектральное значение  его правой части равно
его правой части равно 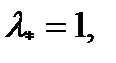 так как в (27) отсутствуют синусы и косинусы. Характеристическое уравнение
так как в (27) отсутствуют синусы и косинусы. Характеристическое уравнение  имеет два различных корня
имеет два различных корня  Спектральное значение не совпадает с ними, и поэтому частное решение уравнения (27) следует искать в виде (см. п.2 алгоритма 21)
Спектральное значение не совпадает с ними, и поэтому частное решение уравнения (27) следует искать в виде (см. п.2 алгоритма 21)  Подставляя это в уравнение (27), имеем
Подставляя это в уравнение (27), имеем  Значит,
Значит, 
Спектральное значение правой части уравнения (28) равно  Оно является корнем кратности
Оно является корнем кратности  характеристического уравнения, поэтому частное решение уравнения (28) следует искать в виде (см. п.3 алгоритма 2):
характеристического уравнения, поэтому частное решение уравнения (28) следует искать в виде (см. п.3 алгоритма 2):  Вычисляя производные
Вычисляя производные


и подставляя их в уравнение (28), получаем тождество
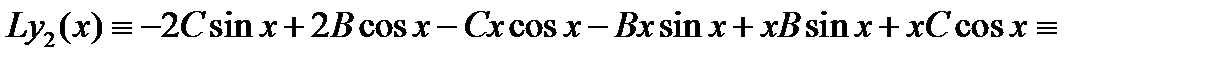

или  Приравнивая здесь коэффициенты при
Приравнивая здесь коэффициенты при 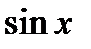 и
и  , получаем
, получаем

Значит, частное решение уравнения (28) имеет вид  Согласно принципу суперпозиции частное решение уравнения (26) является суммой частных решений
Согласно принципу суперпозиции частное решение уравнения (26) является суммой частных решений 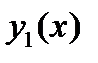 и
и  т.е.
т.е. 
Пo корням  характеристического уравнения
характеристического уравнения  строим общее решение соответстующего однородного уравнения
строим общее решение соответстующего однородного уравнения 
 и общее решение исходного неоднородного уравнения (28):
и общее решение исходного неоднородного уравнения (28):
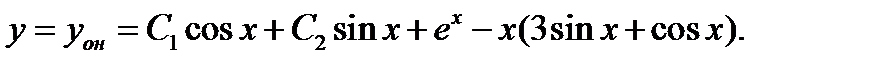

Найдем теперь интегральную кривую, удовлетворяющую начальным условиям  Дифференцируя (29), найдем, что
Дифференцируя (29), найдем, что
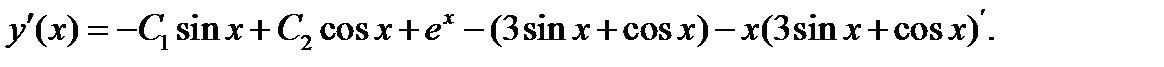

Подчиняя (29) и (30) начальным условиям  будем иметь
будем иметь

Cледовательно, искомая интегральная кривая задаётся уравнением

Замечание. Частное решение уравнення (26) можно вычислить с помощью интеграла (см.  ):
): 
Лекция 6. Комплексные числа и действия над ними. Функции комплексного переменного. Предел и непрерывность. Элементарные функции комплексного переменного и действия над ними
 Комплексные числа и действия над ними были определены ранее (см. лекцию 4). Напомним их. Комплексными числами называют числа вида
Комплексные числа и действия над ними были определены ранее (см. лекцию 4). Напомним их. Комплексными числами называют числа вида  где
где 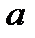 и
и  – действительные числа,
– действительные числа,  мнимая единица (
мнимая единица (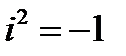 ). При этом число
). При этом число  называется действительной частью, а число
называется действительной частью, а число  – мнимой частью комплексного числа
– мнимой частью комплексного числа  . Число
. Число 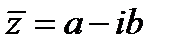 называется сопряженным к числу
называется сопряженным к числу  а неотрицательное число
а неотрицательное число  называется модулем числа
называется модулем числа  . Множество всех комплексных чисел обозначают буквой
. Множество всех комплексных чисел обозначают буквой  Каждому комплексному числу
Каждому комплексному числу  соответствует единственная точка
соответствует единственная точка  . При этом ось
. При этом ось  называется действительной осью, с ось
называется действительной осью, с ось  – мнимой осью. Сама плоскость
– мнимой осью. Сама плоскость  называется комплексной плоскостью; ее тоже обозначают буквой
называется комплексной плоскостью; ее тоже обозначают буквой  Угол
Угол  называется аргументом}комплексного числа
называется аргументом}комплексного числа  . Ясно, что аргумент определяется неоднозначно. Главным значением аргумента называется угол
. Ясно, что аргумент определяется неоднозначно. Главным значением аргумента называется угол  лежащий в пределах
лежащий в пределах 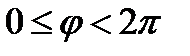 (или в пределах
(или в пределах  ). Главное значение аргумента обозначается так:
). Главное значение аргумента обозначается так:  . Из рис. 1 видно, что
. Из рис. 1 видно, что  Значит, комплексное число можно записать еще в виде
Значит, комплексное число можно записать еще в виде  Эта форма называется тригонометрической формой числа
Эта форма называется тригонометрической формой числа  , а его первоначальная форма
, а его первоначальная форма  --алгебраической формой комплексного числа
--алгебраической формой комплексного числа  . Если воспользоваться формулой Эйлера
. Если воспользоваться формулой Эйлера  то можно получить еще одну форму комплексного числа
то можно получить еще одну форму комплексного числа  называемую показательной формой числа
называемую показательной формой числа  . Понятие комплексной экспоненты и связанная с ней формула Эйлера будут даны немного позднее.
. Понятие комплексной экспоненты и связанная с ней формула Эйлера будут даны немного позднее.
Два комплексных числа называются равными, если равны одновременно порознь действительные и мнимые части этих чисел, т.е.
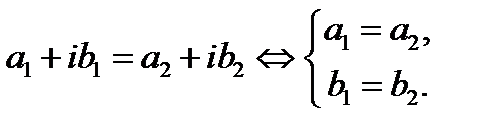
Действия над комплексными числами определяются равенствами:





Умножение комплексных чисел (и их деление) лучше производить в тригонометрической форме:


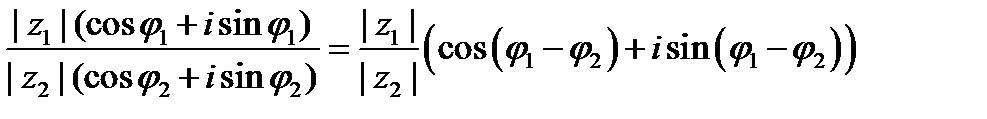

(эти формулы легко получить, используя равенства 1-2). Отсюда вытекает следующее равенство

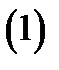
Действительно, применяя первую из предыдущих формул  раз, будем иметь
раз, будем иметь

Дата публикования: 2014-11-04; Прочитано: 687 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
