 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Властивості та графіки тригонометричних функцій
|
|
Властивості та графік функції 
1. Область визначення – уся числова пряма, тобто 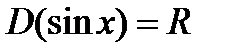 ;
;
2. Область значень – відрізок  , тобто
, тобто  ;
;
3. Функція  – непарна, тобто
– непарна, тобто  ; графік симетричний відносно початку координат;
; графік симетричний відносно початку координат;
4. Функція періодична з основним періодом  ;
;
5. Нулі функції:  при
при  ,
,  ;
;
6. Інтервали знакосталості:
А)  , якщо
, якщо  ,
,  ;
;
Б)  , якщо
, якщо  ,
,  ;
;
7. Інтервали зростання й спадання:
А) Функція  зростає на проміжках
зростає на проміжках 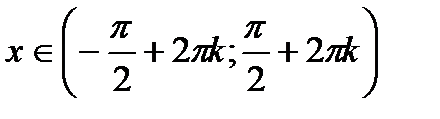 ,
,  ;
;
Б) Функція  спадає на проміжках
спадає на проміжках 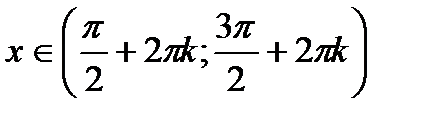 ,
,  ;
;
8. Екстремуми функції:
А)  при
при  ,
,  ;
;
Б)  при
при 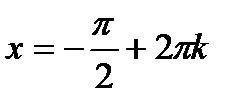 ,
,  ;
;
9. Функція  є обмеженою,
є обмеженою,  .
.
Графік функції  називається синусоїдою, він показаний на рис. 2.
називається синусоїдою, він показаний на рис. 2.
 Рис. 2
Рис. 2
Властивості та графік функції 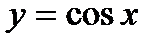
1. Область визначення – уся числова пряма, тобто  ;
;
2. Область значень – відрізок  , тобто
, тобто  ;
;
3. Функція  – парна, тобто
– парна, тобто  ; графік симетричний щодо осі Оу;
; графік симетричний щодо осі Оу;
4. Функція періодична з основним періодом  ;
;
5. Нулі функції:  при
при  ,
,  ;
;
6. Інтервали знакосталості:
А)  , якщо
, якщо 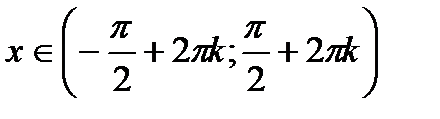 ,
,  ;
;
Б)  , якщо
, якщо 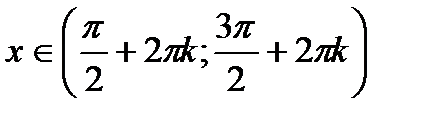 ,
,  ;
;
7. Інтервали зростання і спадання:
А) Функція  зростає на проміжках
зростає на проміжках  ,
,  ;
;
Б) Функція  спадає на проміжках
спадає на проміжках  ,
,  ;
;
8. Екстремуми функції:
А)  при
при  ,
,  ;Б)
;Б)  при
при  ,
,  ;
;
9. Функція  є обмеженою,
є обмеженою,  .
.
Графік функції  називається косинусоїдою, він показаний на рис. 3.
називається косинусоїдою, він показаний на рис. 3.
 Рис. 3
Рис. 3
Властивості та графік функції 
1. Область визначення – множина усіх дійсних чисел, крім чисел виду  ,
,  , тобто
, тобто  ,
,  ;
;
2. Область значення – вся числова пряма, тобто  ;
;
3. Функція  – непарна, тобто
– непарна, тобто 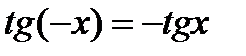 , графік симетричний відносно початку координат;
, графік симетричний відносно початку координат;
4. Функція періодична з основним періодом  ;
;
5. Нулі функції  при
при  ,
,  ;
;
6. Інтервали знакосталості:
А)  , якщо
, якщо  ,
,  ;
;
Б)  , якщо
, якщо  ,
,  ;
;
7. Інтервали зростання і спадання: функція  зростає на проміжках
зростає на проміжках 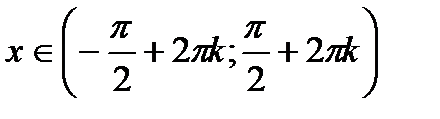 ,
,  ;
;
8. Функція  екстремумів не має;
екстремумів не має;
9. Функція  не обмежена.
не обмежена.
Графік функції  називається тангенсоїдою, він показаний на рис. 4.
називається тангенсоїдою, він показаний на рис. 4.
Прямі 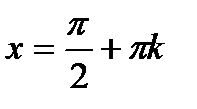 ,
,  називаються вертикальними асимптотами графіка функції
називаються вертикальними асимптотами графіка функції 
 Рис. 4
Рис. 4
Властивості та графік функції 
1. Область визначення – множина усіх дійсних чисел, крім чисел виду  ,
,  , тобто
, тобто  ,
,  ;
;
2. Область значень – вся числова пряма, тобто  ;
;
3. Функція  – непарна, тобто
– непарна, тобто  , графік симетричний відносно початку координат;
, графік симетричний відносно початку координат;
4. Функція періодична з основним періодом  ;
;
5. Нулі функції:  при
при  ,
,  ;
;
6. Інтервали знакосталості:
А)  , якщо
, якщо  ,
,  ;
;
Б)  , якщо
, якщо  ,
,  ;
;
7. Інтервали зростання і спадання: функція  спадає на проміжках
спадає на проміжках  ,
,  ;
;
8. Функція  екстремумів не має;
екстремумів не має;
9. Функція  необмежена.
необмежена.
Графік функції  називається котангенсоїдою, він показаний на рис. 5. Прямі
називається котангенсоїдою, він показаний на рис. 5. Прямі  ,
,  називаються вертикальними асимптотами графіка функції
називаються вертикальними асимптотами графіка функції  .
.
 Рис. 5
Рис. 5
42. Побудуйте графіки функцій:
1)  ; 2)
; 2) 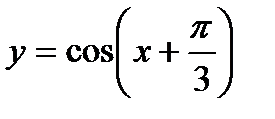 ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9) 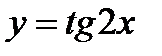 ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  .
.
43. Використовуючи властивості функцій  порівняйте числа:
порівняйте числа:
1)  і
і  ; 2)
; 2)  і
і  ;
;
3)  і
і  ; 4)
; 4)  і
і  ;
;
5)  і
і  ; 6)
; 6)  і
і  ;
;
7) 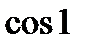 і
і  ; 8)
; 8)  і
і  ;
;
9)  і
і  ; 10)
; 10)  і
і  ;
;
11)  і
і  ; 12)
; 12) 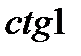 і
і  .
.
44. Розташуйте числа у порядку зростання:
1) 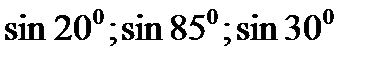 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
45. Побудуйте графік функції  на проміжку
на проміжку  та знайти:
та знайти:
1) значення  , якщо
, якщо  ;
;
2) значення  , якщо
, якщо  ;
;
3) проміжок, де функція спадає.
46. Побудуйте графік функції  на проміжку
на проміжку 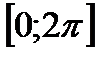 та знайти:
та знайти:
1) значення 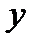 , якщо
, якщо  ;
;
2) значення  , якщо
, якщо 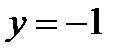 ;
;
3) проміжок, на якому функція зростає.
47. Побудуйте графік функції  на проміжку
на проміжку  та знайти:
та знайти:
1) значення  , якщо
, якщо  ;
;
2) значення  , якщо
, якщо  ;
;
3) проміжок, на якому функція спадає.
48. Побудуйте графік функції  на проміжку
на проміжку 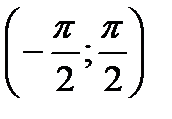 та знайти:
та знайти:
1) значення  , якщо
, якщо  ;
;
2) значення  , якщо
, якщо  ;
;
3) проміжок, на якому функція зростає.
49. Побудуйте графіки функцій:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  .
.
до змісту
Дата публикования: 2014-11-04; Прочитано: 2648 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
