Пример 1. Векторы заданы своими координатами в некотором базисе

Векторы заданы своими координатами в некотором базисе 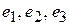. Показать, что векторы сами образуют базис, и найти координаты вектора x в этом базисе.

Решение. Составим матрицу перехода от базиса 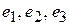к системе векторов :

,

она невырожденная, значит векторы линейно независимы и могут образовывать базис трёхмерного пространства. Тогда

Найдём координаты вектора в базисе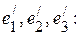

Следующая теорема устанавливает связь между матрицами одного и того же линейного оператора, заданными в разных базисах.

ТЕОРЕМА (о связи матриц линейного оператора). Пусть 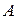и 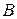– матрицы линейного оператора 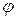в базисах и соответственно и матрица перехода о первого базиса ко второму. Тогда 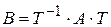(матрицы 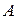и 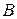называются подобными).

ДОКАЗАТЕЛЬСТВО. Если 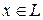, то обозначим через и столбцы из координат вектора в первом и во втором базисах, а через 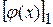и координаты образа этого вектора в первом и во втором базисах.. Из равенства (2) имеем

Из равенства (1) получаем

и .

Из этих трех равенств заключаем, что

.

Но откуда

.

Домножая обе части этого равенства на слева, получаем равенство

Которое имеет место при любом векторе 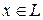. Это означает равенство матриц 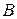и . □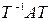

В доказательстве теоремы молчаливо использовался тот факт, что если для любого вектора х выполнено , то 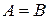. Предлагается его доказать читателю.

Пример 2. Линейный оператор 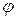в базисе 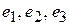имеет матрицу . Найти его матрицу 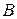в базисе

Решение. Составим матрицу перехода от базиса 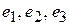к базису :

Найдём обратную матрицу для :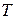

.

Тогда